Okrąg wpisany w trójkąt Misia: 16. Długości dwóch boków trójkąta wynoszą 3 cm i 5 cm, a promień okręgu wpisanego w ten trójkąt jest równy 1 cm. Oblicz długość trzeciego boku trójkąta. 17. Ramiona kąta o mierze 60^o przecięto prostą l prostopadłą do jednego z ramion. Następnie wpisano w ten okrąg dwa koła, każde styczne do jego ramion i do prostej l. Wyznacz stosunek pól tych kół. Proszę bardzo o pomoc. Jeżeli to ułatwi sprawę to podaję odpowiedzi: 16. 4 cm lub 2+2√5 cm 17. 7−4√3 Proszę o rozwiązanie, nie korzystając z twierdzenia sinusów

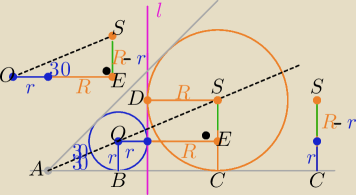
E: Mamy wyznaczyć:

πR2		R
	= (		)2
πr2		r

W trójkącie OES

|SE|		R−r		1
	= tg30o ⇒		=		⇒ √3R−√3r=R+r
|OE|		R+r		√3

	R		√3+1		(√3+1)2
to: R(√3−1)= r(√3+1) ⇒		=		=		= 2+√3
	r		√3−1		3−1

	R
(		)2= (2+√3)2= 7+4√3
	r

	r		1
(		)2=		= 7−4√3
	R		7+4√3

Mila: 16 rozwiązane.