planimetria
nie: długości dwóch boków trójkąta wynoszą 3 cm i 5 cm,a promień okręgu wpisanego w ten trójkąt jest
równy 1 cm. Oblicz długość trzeciego boku trójkąta
7 kwi 18:27
Jack: c = a+b − 2 r
7 kwi 18:29
Jack: a nie, bo nie jest prostokaty...
7 kwi 18:37
Metis:
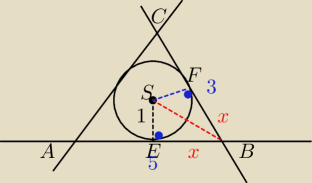
7 kwi 18:46
nie: przykro mi ale i tak dalej nie wiem
7 kwi 19:08
`: prosz podpowiedz coś
7 kwi 20:24
Metis: Trójkąty BES i BSF są podobne. Cecha bkb.
7 kwi 20:27
`: chyba przystające? ale co ztego
7 kwi 20:33
Jack:
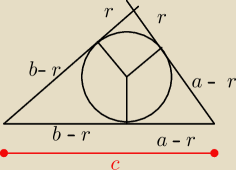
wiesz, ze r = 1
a = 3
b = 5
zatem
c = a+b − 2r = 8 − 2 = 6
7 kwi 20:39
Jack: juz nwm, czy to zle czy nie...nie masz odp?>
7 kwi 20:40
Metis: Ja miałem inny pomysł na to zadanie , ale twój sposób ciekawszy

7 kwi 20:41
Jack: tylko moj zachodzil dla prostokatnego...a dla normalnego to juz sam nwm...
7 kwi 20:42
`: niestety odp jest inna: 4 lub 2+2√5
7 kwi 20:46
Metis: No tak Jack − tam nie ma kąta prostego!
7 kwi 20:51
Metis: Niech |SB|= y , wtedy:
(x−5)2+1=y2 oraz (x−3)2+1=y2
Wylicz x.
Potem z jakiejkolwiek funkcji policzymy kąt. Wtedy będzie prościej.
7 kwi 20:53
Mila:
Skąd masz to zadanie?
Czy masz odpowiedź?
7 kwi 20:58
`: Zadanie z 2 cz. zbioru zadań Nowa Era dla szkół średnich. Odpowiedź do zadania: 4 lub 2+2√5.
7 kwi 21:24
Mila:
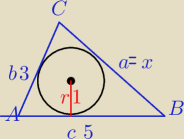
2<x<8
P
Δ=p*r
Ze wzoru Herona :
P
Δ=
√p*(p−a)*(p−b)*(p−c)⇔
P
Δ=
√(4+x2)*(4+x2−5)*(4+x2−3)*(4+x2−a)⇔
P
Δ=
√(4+x2)*(x2−1)*(x2+1)*(4−x2)
Porównujemy pola (1) i (2)
| | x | |
4+ |
| =√(4+x2)*(x2−1)*(x2+1)*(4−x2) /2 |
| | 2 | |
| | x | | x | | x2 | | x2 | |
(4+ |
| )2=(4+ |
| )*( |
| −1)*(4− |
| ⇔ |
| | 2 | | 2 | | 4 | | 2 | |
| | x | | x | | x2 | | x2 | |
(4+ |
| )2−(4+ |
| )*( |
| −1)*(4− |
| =0 |
| | 2 | | 2 | | 4 | | 2 | |
| | x | | x | | x3 | | x | |
(4+ |
| )* (4+ |
| −x2+4+ |
| − |
| )=0⇔ |
| | 2 | | 2 | | 8 | | 2 | |
x
3−8x
2+64=0
W(4)=64−8*16+64=0
Schemat Hornera:
1 −8 0 64 x=4
1 −4 −16 0
x
3−8x
2+64=(x−4)*(x
2−4x−16)=0
rozwiążcie teraz równanie kwadratowe
(x
2−4x−16)=0
7 kwi 21:28
Mila:
Pewnie można poszukać zależności w Δ, ale może jutro podam inny sposób,
chyba, że sami znajdziecie wcześniej.
7 kwi 21:34
Mila:
Metis, Jack co z Wami?
7 kwi 22:35
Kacper:
Inny sposób to skorzystać z tw cosinusów.

Jak nikt go nie doda, to jutro wpiszę.
Ładnie się liczy

7 kwi 22:38
Mila:
Witaj
Kacper, nie chciało mi się szukać zależności.
Pewnie w zbiorze jest jakaś wskazówka,
a przynajmniej jakiś ciąg zadań powiązanych z sobą.
Autor już nie interesuje się.
Napisz jutro swój sposób.

7 kwi 23:08
Kacper:
Mam ten zbiór. Jest tylko odpowiedź podana, ale przyjrzę się poprzednim zadaniom.

8 kwi 07:44
Jack: na razie musze sie za fize wziac...
8 kwi 15:09
Kryś: Mila masz blad bo nie spotegiqalas 4 ani 2 w pierwiastku z x
28 maj 18:35
Kryś: A nie inaczej czemu spotegowalas x?
28 maj 18:37
Mila:
Tam mam w dwóch linijkach błędny zapis . Pewnie przy przepisywaniu z kartki, kopiowaniu)
| | x | |
niepotrzebny 2 i brak nawiasu w ostatnim czynniku. Powinno być... (4− |
| ) |
| | 2 | |
x>0
| | x | |
4+ |
| =√(4+x2)*(x2−1)*(x2+1)*(4−x2)⇔ |
| | 2 | |
| | x | |
4+ |
| =√(4+x2)*(x24−1)*(4−x2) /2 |
| | 2 | |
| | x | | x2 | | x | |
(4+ |
| )2=(4+x2)*( |
| −1)*(4− |
| )⇔ |
| | 2 | | 4 | | 2 | |
| | x | | x2 | | x | | x | |
(4+ |
| )2−(4+x2)*( |
| −1)*(4− |
| )=0 wyłączam (4+ |
| ) |
| | 2 | | 4 | | 2 | | 2 | |
| | x | | x | | x3 | | x | |
(4+ |
| )*[4+ |
| −(x2− |
| −4+ |
| ]=0 |
| | 2 | | 2 | | 8 | | 2 | |
| | x | | x | | x3 | | x | |
4+ |
| =0 lub (4+ |
| −x2+ |
| +4− |
| )=0 |
| | 2 | | 2 | | 8 | | 2 | |
| | x3 | |
x=−8∉D lub |
| −x2+8=0 /*8 |
| | 8 | |
x
3−8x+64=0
dalej dobrze.
x=4 lub x=2+2
√5
28 maj 19:00
Mila:
Znów zgubiłam kwadrat.
x3−8x2+64=0
28 maj 19:02
Kryś: Nie ogarniam co sie dzieje po wylaczeniu
28 maj 19:30
Kryś: Skad sie x2 wzial
28 maj 19:31
Kryś: I reszta tez z reszta
28 maj 19:31
Mila:
Napisz która linijka z 19:2 jest niejasna. O jaki kwadrat chodzi?
28 maj 20:24

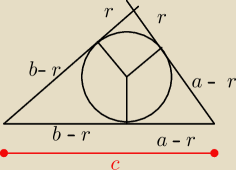 wiesz, ze r = 1
a = 3
b = 5
zatem
c = a+b − 2r = 8 − 2 = 6
wiesz, ze r = 1
a = 3
b = 5
zatem
c = a+b − 2r = 8 − 2 = 6

 2<x<8
PΔ=p*r
2<x<8
PΔ=p*r
 Jak nikt go nie doda, to jutro wpiszę.
Ładnie się liczy
Jak nikt go nie doda, to jutro wpiszę.
Ładnie się liczy 

