kotecek Kotecek : 4sinx+7cosx=4 a)nie ma rozwiązań b) ma dokładnie jedno rozwiązanie rzeczywiste c)ma dokładnie dwa rozwiązania rzeczywiste d) ma więcej niż dwa rozwiązania rzeczywiste

ICSP: d

Metis: Trzeba rozwiązać

Kotecek : jakaś wskazówka?

ICSP:

	π
x =		+ 2kπ jest rozwiązaniem.
	2

Kotecek : jeż chyba wiem

Kotecek : czy 4= 4sin²x +4 cos²x

Kotecek : jednak nie to nic nie da

ICSP: Tak.

Kotecek : wzory redukcyjne?

ICSP: Przecież podałem Ci jedno z rozwiązań.

Kotecek : a jak to równanie rozwiązać

ICSP: Nie ma polecenia aby rozwiązać równanie. Masz tlyko znaleźć ilość rozwiazań a nie podać same rozwiązania.

Mila: Myślenie: Równanie może mieć rozwiązanie jeżeli cosx=0⇔

	π
x=		+2kπ
	2

Równanie ma nieskończenie wiele rozwiązań.

Kotecek : dziękuje wszystkim za pomoc

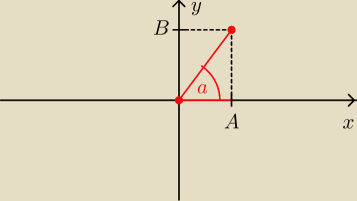
Dżin: Przy takich odpowiedziach wystarczy wyznaczyć zbiór wartości funkcji f(x)=4sinx+7cosx f(x) da się przedstawić w postaci f(x)=√4²+7²sin(x+α) a wynika to ze wzoru A*sinx+B*cosx=√A²+B²sin(x+α) gdzie α jest kątem "a" przedstawionym na rysunku Zbiór wartości funkcji f to (−√65; √65), więc funkcja y=4 przecina ów sinusoidę w nieskończenie wielu miejscach, co wynika z interpretacji geometrycznej, tym samym dane równanie ma więcej niż dwa rozwiązania rzeczywiste