Udowodnij , że trójkąty są przystające
Marysia:
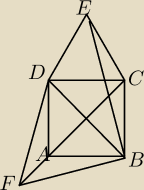
Na boku CD kwadratu ABCD zbudowano trójkąt równoboczny DCE, zaś na przekątnej BD
kwadratu trójkąt równoboczny BDF w taki sposób żeby wierzchołek A kwadratu
znalazł się we wnętrzu trójkąta BDF.
Udowodnij, że trójkąty BDE i CBF sa przystające
6 kwi 23:47
Marysia:
7 kwi 00:10
Marysia: Nadal nie wiem jak to ugryźć. Ktoś, coś?
7 kwi 11:12
Wiem:
Po prostu widzisz
Δ
BDE :∡DEB = α
h−wysokość z D
| h | | a | | h | | a√2 | |
| = |
| ∧ |
| = |
| ;∡BDE=105o(łapiesz?) |
| sinα | | sin90o | | sin(75−α) | | sin90o | |
| | sin75o | |
tgα = |
| ,tgα = 1,α=45o |
| | cos75o +√2/2 | |
DB=a ;∡DEB =45
o ∧ CB=a ;∡FCB =45
o c.n.d
7 kwi 11:22
jc: Obróć wokół punktu D o 60o w prawo trójkąt BDE.
D pozostanie na miejscu, B przejdzie na F, a E na C, czyli BDE i FDC są przystające.
Teraz odbij trójkąt FCD względem prostej FC. Otrzymasz trókjąt FBC, a więc trójkąty
FCD i FBC są przystające. Relacja przystawania jest przechodnia. Dlatego trójkąty
BDE i FBC są przystające.
7 kwi 11:35
exit:
marysia i jc to to samo tałatajstwo co np. daras,zyxel,itd.Sam sobie wystawia zadania,a potem
przepisuje rozwiązania
7 kwi 14:45
jc: Nie wstyd Ci exit, tak nieładnie pisać?
7 kwi 16:43
exit: ale to święta prawda
7 kwi 17:09
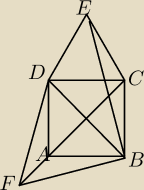 Na boku CD kwadratu ABCD zbudowano trójkąt równoboczny DCE, zaś na przekątnej BD
kwadratu trójkąt równoboczny BDF w taki sposób żeby wierzchołek A kwadratu
znalazł się we wnętrzu trójkąta BDF.
Udowodnij, że trójkąty BDE i CBF sa przystające
Na boku CD kwadratu ABCD zbudowano trójkąt równoboczny DCE, zaś na przekątnej BD
kwadratu trójkąt równoboczny BDF w taki sposób żeby wierzchołek A kwadratu
znalazł się we wnętrzu trójkąta BDF.
Udowodnij, że trójkąty BDE i CBF sa przystające