Okresl zbiór warości i przedziały monotonicznośći funkcji Ola: Określ zbiór warości i przedziały monotonicznośći funkcji f(x)=x²+8x−15

Janek191: a = 1 b = 8 c = − 15

	−b		−8
p =		=		= − 4
	2a		2

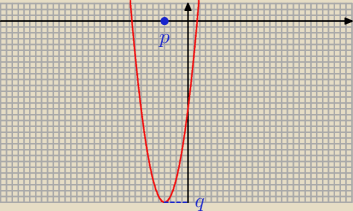
q = f(p) = f(−4) = (−4)² + 8*(−4) − 15 = 16 − 32 − 15 = − 31 a = 1 > 0 więc zbiór wartości ZW = < q ; + ∞ ) = < − 31, + ∞) Dla x < p funkcja maleje, a dla x > p funkcja rośnie.

yht: parabola ∪ a=1, b=8, c=−15

	−b		−8
p=		=		=−4
	2a		2*1

przedziały monotoniczności: malejąca dla x∊(−∞,−4) rosnąca dla x∊(−4,+∞) zbiór wartości: q=f(p)=f(−4)=(−4)²+8*(−4)−15=16−32−15=−16−15=−31 zbiór wartości: y∊<−31,+∞) podsumowując monotoniczność zależy od p zbiór wartości zależy od q jeśli parabola ∪ to: monotoniczność: rosnąca dla x∊(p,+∞), malejąca dla x∊(−∞,p) zbiór wartości to y∊<q,+∞) jeśli parabola ∩ to: monotoniczność: rosnąca dla x∊(−∞,p) , malejąca dla x∊(p,+∞) zbiór wartości to y∊(−∞,q>

5-latek : Janek To jest w czystej postaci lenistwo Takie zadania sa w internecie i w książce .

Ola: dzięki