Dla jakich wartości parametru m prosta y=mx-m-2 qwerty: Dla jakich wartości parametru m prosta y=mx−m−2 ma co najmniej jeden punkt wspólny z prostokątem ABCD, jeżeli A(0,0), B(1,0). C(1,2), D(0,2)? Próbowałam liczyć to w ten sposób, że y∊<0,2> i x∊<0,1>, ale ciągle wychodzi mi wynik m∊(−∞;−4>, a powinno być m∊(−∞;−2>. Może ktoś z was mógłby mi pokazać jak to prawidłowo policzyć?

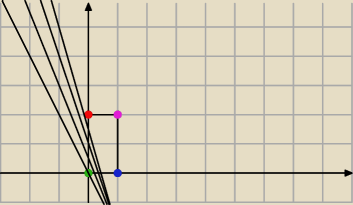
wredulus_pospolitus: 1) m>0 czerwona kropa −m−2 ≤ 2 −> −m ≤ 4 −> m ≥ −4 niebieska kropka f(1) ≥ 0 −> m − m − 2 ≥ 0 −> −2 ≥ 0 ... sprzeczne Wniosek −−− żadna funkcja rosnąca 'nie załapie' się na prostokąt. 2) m = 0 y = −2 <−−− 'nie łapie' się 3) m < 0 fioletowa kropka m−m−2 ≤ 2 −> −2≤ 2 <−−− spełnione zawsze zielona kropka −m−2 ≥ 0 −> m ≤ −2 Czyli rozwiązanie będzie dla m∊(−∞;−2>

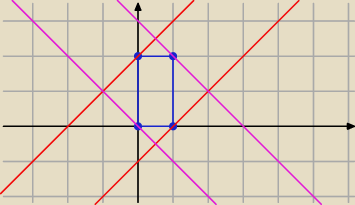
Janek191: 1) m> 0 2) m < 0

Lukasz: @wredulus_pospolitus Dlaczego funkcja (przy czerwonej kropie) m≥−4 nie łapie się na prostokąt?

Lukasz: I czy my bierzemy wspólną część wszystkich przedziałów dla m ? czy jak bierzemy rozwiązanie?

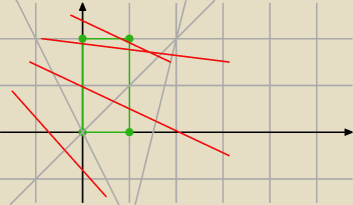
a7: np. dla −m−2=0 −m=2 czyli m=−2 prosta y=−2x ma jeden punkt przecięcia z prostokątem dla m=0 mamy prostą y=−2, która nie ma punktów wspólnych z prostokątem dla −m−2>0 ( czyli m<−2) i(jednocześnie) funkcji rosnącej m>0 sprzeczność dla −m−2<0 i m>0(czyli) funkcji rosnącej f(1) musiałaby być większa lub równa zeru czyli jak pisał wredulus żadna funkcja rosnąca nie daje przecięcia z prostokątem w co najmniej jednym punkcie dla m<0 (funkcji malejącej) wartość funkcji dla x=0 czyli f(0) musi być większe od zera i (jednocześnie) f(1)≤2 (czerwone proste) f(0)=−m−2≥0 czyli −m≥2 ⇒m≤−2 i teraz f(1)=m−m−2≤2 ⇒−2≤2 co jest zawsze prawdą ponieważ było "i" więc liczy się część wspólna czyli m≤−2 czyli m∊(−∞,−2≥