Równanie stycznej do okręgu galanonim: Wyznacz równania stycznych do okręgu o równaniu x² + y² −8y = 4 przechodzących przez punkt A=(−2,−1) wyznaczyłem sobie najpierw środek a następnie promień, następnie wiemy że promień pada pod kątem prostym do stycznej więc wyznaczyłem równanie prostej przechodzącej przez środek i punkt (−2,−1) a następnie wiemy że współczynnik a stycznej bedzie odwrotny i z przeciwnym znakiem. NIestety rónanie w odpowiedziach jest błędne. Proszę mi wyjaścnić czy można tak robić

wredulus_pospolitus: pokaż swoje obliczenia

Jerzy: Proste mają równanie: y = a(x+2) − 1 , Podstaw do równania okręgu i nałóż warunek...jedno rozwiązanie

jc: Do czego potrzebujesz prostej przechodzącej przez środek okręgu i dany punkt? "wiemy że współczynnik a stycznej bedzie odwrotny i z przeciwnym znakiem" Do czego odwrotny? A jak rozwiązać zadanie? Widzę co najmniej 3 sposoby. 1. Znaleźć proste przechodzące przez A, posiadające dokładenie jeden punkt wspólny z okręgiem. 2. Znaleźć proste przechodzące przez A, których odległość od środka okręgu równa jest promieniowi okręgu. 3. Ze wszystkich stycznych wybrać te, które przechodzą przez punkt A.

galanonim: x{2} + y{2} − 8y = 4 c= −4, −2b=−8 b= 4 a=0 S(0,4) r² = 16+4 r= 2√2 y= ax +b −1 = −2a +b 4=b −5= −2a

	5
a=
	2

	5
y=		x + 4
	2

5
	* a2 = −1
2

	2
a2= −
	5

	2		4
y= −		x − 1
	5		5

jc: Jerzy napisał jak zacząć wg pierwszego sposobu, kontynuuj.

galanonim: Wiemy że jeżeli prosta jest prostopadła a w tym przypadki promień pada pod kątem prostym do stycznej to a1*a2 = −1

Jerzy: A co to ma do rzeczy ?

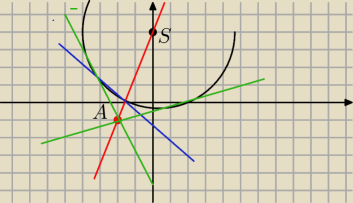
5-latek : (x−0)²+(y−4)²= 20 Popatrz na rysunek ty zrobiles takie cosik ( to niebieskie A to nie ma tak być ma być to zielone

jc: galanonim, Jeśli chcesz po swojemu, to możesz zacząć tak x² + y²−8y = 4, x*(x+2) + (y−4)*(y+1) = 0 (x,y) − punkt styczności Pierwsze równanie mówi, że (x,y) leży na okręgu. Drugie, że promień jest prostopadły do odcinka łączącego punkt styczności z punktem A.