parametr
5-latek : napisze jeszcze raz
mam równanie kwadratowe z parametrem . Maja być dwa rozne rozwiązania spelniajace warunek
|x1|+|x2|<k
Chodzi mi tylko o to ze po podniesieniu obustronnie do potęgi drugiej dostane miedzy innymi
+2|x1*x2|
Pewnie mam gdzie to w książkach ale musialem je wynieść
6 kwi 08:38
5-latek : Chodzi o to jak z tego skorzystać ze wzorow Vieta
6 kwi 08:41
Jerzy:
Cześć

o co chodzi ?
6 kwi 08:57
Jerzy:
x2*x2 = c/a
6 kwi 09:06
5-latek : Po podniesieniu do potęgi drugiej mam
x12+x22+2|x1*x2|<k2
teraz x12+x22= (x1+x2)2−2x1*x2
A co z tym 2|x1*x2|?
6 kwi 09:07
Jerzy:
Nic = 2*|c/a|
6 kwi 09:14
5-latek : Wezmy to równanie które napisał kolega fineasz
x2+2mx+1=0
spelniac rozne rozwiązania maja warunek
|x1|+|x2|<2√11
Po podniesieniu do kwadratu
(x1+x2)2−2x1*x2+2|x1*x2|
Tutaj |x1*x2|=|1| ale |1|=1 lub (−1)
czyli
dostaniemy dwie nieronosci
(x1+x2)2−2+2<44
i druga
(x1+x2)2 −2−2<44
Teraz czesc wspolna rozwiazan i warunek oczywiście na delte i mamy zbior parametru m
6 kwi 09:25
5-latek :
6 kwi 09:41
Jerzy:
Skąd .. |c/a| = |1| = 1 przecież c i a są ustalone ( dane )
6 kwi 09:54
PW:
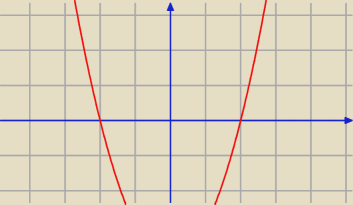
Nie chce mi się omawiać szczegółowo, ale poddam pomysł. Może trzeba pobawić się przesuwaniem
paraboli.
Dopóki jest symetryczna względem osi OY, to żądanie
(1) |x
1| + |x
2| < 2
√11
jest równoważne żądaniu
(2) x
2 <
√11
(dodatnie miejsce zerowe ma być mniejsze od
√11.
Jeżeli przesuniemy parabolę "niewiele", to znaczy tak by w dalszym ciągu miejsca zerowe były
różnych znaków, to wartość |x
1| + |x
2| nie zmieni się (odległość od zera jednego miejsca
zerowego zmniejszy się, a drugiego o tyle samo się zwiększy). Warunek (2) w dalszym ciągu
odpowiada treści zadania.
Gdy przesuniemy parabolę tak, że oba miejsca zerowe są ujemne lub oba dodatnie, to wiemy jak
warunek (1) zapisać
bez wartości bezwzględnych.
Byłoby to ładne ćwiczenie wykorzystania postaci kanonicznej.
6 kwi 09:58
5-latek : Dobrze
Dziekuje CI bardzo

mam remnont instalacji elektrycznej w domu (pewnie jeszcze z tydzien potrwa )i tak jeszce
zagladam co dokupić jak pojade do miasta
6 kwi 09:59
5-latek : dzień dobry
PW 
Pozdrawiam
Bardzo ciekawe to co napisales . daje to sobie do ulubionych i po remoncie wroce do tego
6 kwi 10:02
 o co chodzi ?
o co chodzi ?
 Nie chce mi się omawiać szczegółowo, ale poddam pomysł. Może trzeba pobawić się przesuwaniem
paraboli.
Dopóki jest symetryczna względem osi OY, to żądanie
(1) |x1| + |x2| < 2√11
jest równoważne żądaniu
(2) x2 < √11
(dodatnie miejsce zerowe ma być mniejsze od √11.
Jeżeli przesuniemy parabolę "niewiele", to znaczy tak by w dalszym ciągu miejsca zerowe były
różnych znaków, to wartość |x1| + |x2| nie zmieni się (odległość od zera jednego miejsca
zerowego zmniejszy się, a drugiego o tyle samo się zwiększy). Warunek (2) w dalszym ciągu
odpowiada treści zadania.
Gdy przesuniemy parabolę tak, że oba miejsca zerowe są ujemne lub oba dodatnie, to wiemy jak
warunek (1) zapisać bez wartości bezwzględnych.
Byłoby to ładne ćwiczenie wykorzystania postaci kanonicznej.
Nie chce mi się omawiać szczegółowo, ale poddam pomysł. Może trzeba pobawić się przesuwaniem
paraboli.
Dopóki jest symetryczna względem osi OY, to żądanie
(1) |x1| + |x2| < 2√11
jest równoważne żądaniu
(2) x2 < √11
(dodatnie miejsce zerowe ma być mniejsze od √11.
Jeżeli przesuniemy parabolę "niewiele", to znaczy tak by w dalszym ciągu miejsca zerowe były
różnych znaków, to wartość |x1| + |x2| nie zmieni się (odległość od zera jednego miejsca
zerowego zmniejszy się, a drugiego o tyle samo się zwiększy). Warunek (2) w dalszym ciągu
odpowiada treści zadania.
Gdy przesuniemy parabolę tak, że oba miejsca zerowe są ujemne lub oba dodatnie, to wiemy jak
warunek (1) zapisać bez wartości bezwzględnych.
Byłoby to ładne ćwiczenie wykorzystania postaci kanonicznej.
 mam remnont instalacji elektrycznej w domu (pewnie jeszcze z tydzien potrwa )i tak jeszce
zagladam co dokupić jak pojade do miasta
mam remnont instalacji elektrycznej w domu (pewnie jeszcze z tydzien potrwa )i tak jeszce
zagladam co dokupić jak pojade do miasta
 Pozdrawiam
Bardzo ciekawe to co napisales . daje to sobie do ulubionych i po remoncie wroce do tego
Pozdrawiam
Bardzo ciekawe to co napisales . daje to sobie do ulubionych i po remoncie wroce do tego