Czworokąt opisany na okręgu

Czworokąt opisany na okręgu Maturzysta: Na czworokącie ABCD opisano okrąg. Przekątne tego czworokąta przecinają się w punkcie P. Wykaż, że kąt APB = kąt ACB + kąt CAD

5 kwi 20:32

Maturzysta: Zły tytuł, czworokąt wpisany do okręgu*

5 kwi 20:33

Maturzysta: Ponawiam się emotka

5 kwi 21:42

Mila: Za chwilę, rysuję.

5 kwi 22:29

Mila:

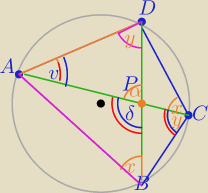
|∡APB| = |∡ACB |+ |∡ CAD| ? Kąty oznaczone tą samą literą mają równe miary jako kąty wpisane oparte na tym samym łuku. W ΔAPBD: α+v+y=180⇔α=180−(v+y) α+δ=180 δ=180−α δ=180−[180−(v+y)] δ=v+y =====

5 kwi 22:39

Maturzysta: Bardzo dziękuję emotka

5 kwi 22:55

Mila:

5 kwi 23:08