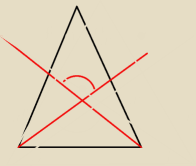
 Bok AB jest podstawą trójkąta równoramiennego ABC. Srodkowe AE i BF przecinają się pod kątem
prostym. Oblicz cosα, gdzie α=ACB
Bok AB jest podstawą trójkąta równoramiennego ABC. Srodkowe AE i BF przecinają się pod kątem
prostym. Oblicz cosα, gdzie α=ACB
 x
x
| A+C | B+C | |||
( | − B) * ( | − A) = 0 | ||
| 2 | 2 |
| A+C | ||
Trzeba to rozumieć tak: | = D to punkt przecięcia środkowej z odcinkiem AC, | |
| 2 |
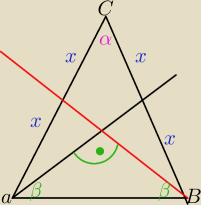
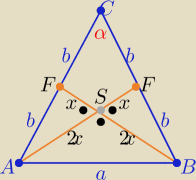 1/ Środkowe w trójkącie dzielą się w stosunku 2:1 licząc od wierzchołka
zatem |AS|=BS|=2x i |FS|=ES|=x , x>0
2/ z treści zadania środkowe są prostopadłe , to
dwa razy tw. Pitagorasa
b2=5x2 i a2=8x2
3/ z tw. kosinusów w ΔABC
1/ Środkowe w trójkącie dzielą się w stosunku 2:1 licząc od wierzchołka
zatem |AS|=BS|=2x i |FS|=ES|=x , x>0
2/ z treści zadania środkowe są prostopadłe , to
dwa razy tw. Pitagorasa
b2=5x2 i a2=8x2
3/ z tw. kosinusów w ΔABC
| (2b)2+(2b)2−a2 | 4 | |||
cosα= | =................... = | |||
| 2*2b*2b | 5 |