Stereometria
kam: W ostrosłupie prawidłowym czworokątnym wszystkie krawędzie maja jadnakową długość rowna 20.
Ostrosłup przecięto płaszczyzną przechodzącą przez środki krawędzi wychodzących z jednego
wierzchołka przy podstawie. Oblicz: a) pole otrzymanego przekroju b)odległość tej płaszczyzny
od punktu wspólnego tych krawędzi.
Pomożecie? Przede wszystkim jak ta płaszczyzna powinna wyglądać?
5 kwi 16:44
Janek191:
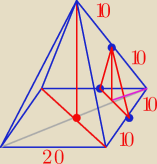
5 kwi 17:10
kam: Wierzchołek przecina krawędz boczna ostrosłupa dokładnie na środku ze względu na fakt że dwa
pozostałe przecinaja też na środku krawedzi podstawy i jest to ostrosłup prawidłowy czy jest
jakieś inne uzasadnienie?
5 kwi 17:16
Janek191:
Wierzchołek nic nie przecina.

5 kwi 17:19
Janek191:
Płaszczyzna przecina .
5 kwi 17:19
Janek191:
1) Oblicz długość przekątnej kwadratu.
2) Oblicz wysokość ostrosłupa
3) Oblicz pole przekroju osiowego
| | 1 | |
4) Z tw. Talesa wynika,że mały Δ jest podobny do przekroju osiowego w skali k = |
| |
| | 2 | |
więc jego pole jest 4 razy mniejsze od pola przekroju osiowego.
5 kwi 17:23
kam: Policzone, dzięki

5 kwi 17:29


