Planimetria Marcinek: Na okręgu o promieniu √3 opisano trapez równoramienny ABCD o dłuższej podstawie AB i krótszej CD. Punkt styczności S dzieli ramię BC tak, że (|CS|)/(|SB|) = 1/3 Oblicz: a) długość ramienia tego trapezu b) cosinus kąta ABD

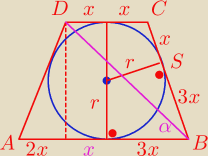
Janek191: Tw. Pitagorasa (2 r )² + ( 2 x)² = (4 x)² (2 √3)² = 16 x² − 4 x² = 12 x² 12 = 12 x² x = 1 c = 4 x = 4*1 = 4 ============= b) I BD I² = ( 2 r)² + ( 4 x)² = (2√3)² + 16 = 12 + 16 = 28 I BD I = 2 √7 więc

	4 x		4		2		2√7
cos α =		=		=		=
	I BD I		2√7		√7		7

=========================

Marcinek: Dziękuje