aaaa Benny: 1. Cenę nart obniżono o 20%, a po miesiącu nową cenę obniżono o dalsze 30%. W wyniku obniżek cena nart zmniejszyła się o: x − cena nart

	1
20%x=		x
	5

	1		4
x−		x=		x − cena nart po pierwszej obniżce
	5		5

	4		6
30%		x=		x
	5		25

4		6		14
	x−		x=		x − cena po obniżkach
5		25		25

	14		11
x−		=		x=44%x − cenę obniżono o 44%
	25		25

2. Liczba ³√(−8)⁻³*16^3/4 jest równa:

	−1
3√(−8)−3*163/4=(−8)−3/3*(24)3/4=		*23=−1
	8

3. Liczba (3−√2)²+4(2−√2)=(9−6√2+2)+8−4√2=11−6√2+8−4√2=19−10√2 4. Iloczyn 2*log_1/39 jest równy: log_1/39=x

	1
(		)x=9
	3

3^−x=3² x=−2 2*log_1/39=2*(−2)=−4 5. Wskaż liczbę, która spełnia równanie |3x+1|=4x 4x>0 ⇒x>0 3x+1=4x lub 3x+1=−4x x=1 lub 7x=−1 − sprzeczność x=1 jest jedynym rozwiązaniem

Benny: 6. Liczby x₁, x₂ są różnymi pierwiastkami równania 2x²+3x−7=0. Suma x₁+x₂ jest równa:

	−b		−3
x1+x2=		=
	a		4

7. Miejscami zerowymi funkcji kwadratowej y=−3(x−7)(x+2) są: Postać iloczynowa funkcji kwadratowej y=a(x−x₁)(x−x₂), więc x₁=7, x₂=−2 8. Funkcja liniowa określona jest wzorem f(x)=ax+6, gdzie a>0. Wówczas spełniony jest warunek: f(1)=a+6 a>0 /+6 a+6>6 f(1)>1 9. Liczba tg30^o−sin30^o jest równa:

	√3
tg30o=
	3

	1
sin30o=
	2

√3		1		2√3		3		2√3−3
	−		=		−		=
3		2		6		6		6

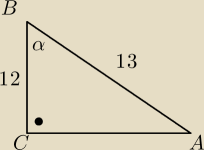
10. W trójkącie prostokątnym ABC odcinek AB jest przeciwprostokątną i |AB|=13 oraz |BC|=12. Wówczas sinus kąta ∡ABC jest równy: |AC|²+|BC|²=|AB|² |AC|²+144=169 |AC|²=25 |AC|=5

	5
sinα=
	13

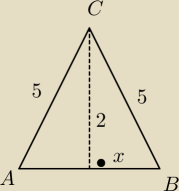
Benny: 11. |AB|=2x 5²=2²+x² x²=25−4 x=√21 2x=|AB|=2√21

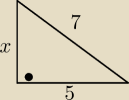
Benny: 12. W trójkącie prostokątnym dwa dłuższe boki mają długość 5 i 7. Obwód tego trójkąta jest równy: 7²=5²+x² x²=24 x=√24=2√6 Obwód=12+2√6

wredulus_pospolitus: Zadanie 1 można było szybciej policzyć: Po pierwszej obniżce cena stanowi 80% wstępnej ceny. Po drugiej obniżce cena stanowi 70% wstępnej (przed tą obniżką) ceny. 'Na kalkulatorze' liczymy więc: 0.8*0.7 = 0.56 <−−− taką cenę mają narty po dokonaniu obu obniżek ... czyli łączna obniżka wynosi 0.44 = 44%

wredulus_pospolitus: Zadanie 4 log_1/39 = −1*log₃9 = −1*2 = −2

	1
własność logarytmów: logab c =		logac
	b

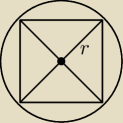
Benny: 13. Pole kwadratu wpisanego w okrąg o promieniu 5 jest równe: 2r − przekątna kwadratu 10=a√2 /()2 100=2a² a²=50 14. Miary kątów czworokąta tworzą ciąg arytmetyczny o różnicy 20^o. Najmniejszy kąt tego czworokąta ma miarę: Suma kątów w czworokącie to 360^o. a₁+a₂+a₃+a₄=360^o a₂=a₁+r a₃=a₁+2r a₄=a₁+3r a₁+a₂+a₃+a₄=4a₁+6r=4a₁+120^o 4a₁+120^o=360^o 4a₁=240^o a₁=60^o − najmniejszy kąt 15.

	2−n
Dany jest ciąg (an) określony wzorem an=(−1)n*		. Wówczas wyraz a5 tego ciągu jest
	n2

równy:

	2−5		−3		3
a5=(−1)5*		=−1*		=
	52		25		25

Benny: @wreduluspospolitus można było. Te zadania nie są dla mnie.

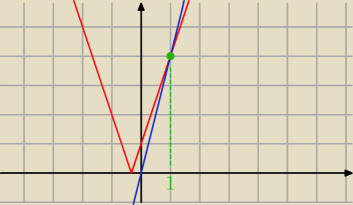
wredulus_pospolitus: Zadanie 5 Mała poprawka (nie wpływająca w tym przypadku na wynik) −> 4x ≥ 0 ⇔ x ≥ 0 druga sprawa −−− można było to 'szybko' graficznie rozwiązać:

wredulus_pospolitus: Aaaaa ... to przepraszam W zad 6 −−− w mianowniku winno być 2.

Benny: 16. Pole powierzchni jednej ściany sześcianu jest równe 4. Objętość tego sześcianu jest równa: Pole powierzchni jednej ściany to pole kwadratu. a²=4 a=2 V=a³=8

Benny: Jasne, dzięki za poprawę. 6.

−b		−3
	=
a		2

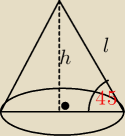
Benny: 17. Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 45^o. Wysokość tego stożka jest równa:

h
	=sin45o
l

	√2
h=l*
	2

h=2√2 18. Wskaż równanie prostej równoległej do prostej o równaniu 3x−6y+7=0 6y=3x+7

	1		7
y=		x+
	2		6

prosta równoległa ma ten sam współczynnik kierunkowy

	1
a=
	2

	1
A. y=		x
	2

Benny: 19. Na okręgu o równaniu (x−2)²+(y+7)²=4 leży punkt: sprawdzam po kolei: A(−2; 5) (−4)²+(12)²=160≠4 B(2; −5) 0²+2²=4 punkt B leży na okręgu