ojojoj ojojoj: W stożek wpisano walec w ten sposób, że dolna podstawa walca zawiera się w dolnej podstawie stożka, a okrąg górnej podstawy walca zawiera się w powierzchni bocznej stożka. Wiadomo, że promień podstawy walca jest trzy razy krótszy od promienia podstawy stożka, a pole przekroju osiowego stożka jest równe 18. Oblicz pole powierzchni bocznej walca.

ojojoj: podbijam

ojojoj: no to jeszcze raz

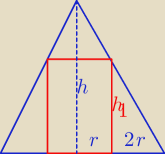
Janek191: Mamy

	6
Po = 0,5 *6r*h = 18 / : 3 ⇒ r*h = 6 ⇒ h =
	r

h1		2r		2		2		2		6		4
	=		=		⇒ 3 h1 = 2 h ⇒ h1 =		h =		*		=
h		3r		3		3		3		r		r

więc pole powierzchni bocznej walca

	4
Pb = 2πr*h1 = 2πr*		= 8π
	r