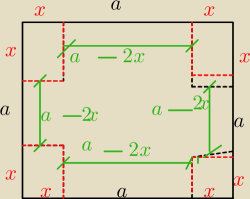
Max i min (kwadratowa 5-latek : zadanie Z kawalka blachy mającego ksztalkt kwadratu o boku dlugosci a wyciac na rogach takie rowne kwadraciki aby po zagięciu brzegow otrzymać prostopadloscienne naczynie o najwiekszsej objetosci Objetosc prostopadloscianu wyraz się wzorem V=a*b*c U nas po wycięciu tych kwadracików objetosc tego naczynia będzie wynosic V= (a−2x)*(a−2x)*x V= (a−2x)²*x V=a²x−4ax²+4x³ Teraz mam liczyc V(x) czy V(a) ? Proszę pokazac

Jerzy: a to wartość stała, a zmienną jest x

5-latek : Już się z Toba witałem wiec V(x)= 4x³−4ax²−a²x V(x)= x(4x²−4ax−a²) Teraz mam zbadac kiedy 4x²−4ax+a² osiąga minimum żeby ta objetosc była najwieksza ? NO to osiąga w wierzchołku tej paraboli

	−(−4a)		1
wiec xnim =		=		a
	8		2

Ale cos nie jest tak bo wtedy a−2x=0

5-latek : Czyli cos robie zle tylko co ?

Jerzy: Liczymy pochodną z V(x)

5-latek : Jerzy Chodzi o to żeby zrobić to bez rachunku różniczkowego

5-latek :

kochanus (z komorki): Maksimum w f(x) nie musi sie pokrywac z maksimum g(x) = x*f(x) Niestety − nie ma tak latwo tutaj

kochanus (z komorki): Po drugie to co w nawiasie jest osiaga MINIMUM dla takiego x (Ramiona paraboli skierowane do gory)

5-latek : Witaj czy do tej pory post 11:05 było dobrze ? Tak ? Teraz moglbys pokazac jak dalej ?

kochanus (z komorki): Jak najbardziej ... tutaj niestety pochodna lub poszukaj w internetach postaci 'kanonicznej' dla wielomianu 3 stopnia ( o ile w ogole taka istnieje) badz jakiegos wzoru do wyliczania wspolrzednych minimum/maksimum lokalnego −−− moze cos jest, nie wiem (nigdy nie potrzebowalem wiec sie nie orientuje, a na komorce szukac nie bede)

5-latek : Dobrze .Poszukam sobie No pewnie ze na komórce nie będziesz specjalnie szukal Znajde może to zadanie w innej książce (ale muszse je teraz wynieść )

5-latek : Znalazlem rozwiązanie podobnego zadania tylko ze tam jest arkusz prostokątny o wymiarach 80X50cm Rozwiazanie tego zadania jest dla mnie w tej chwili niezrozumiale. Wiec na razie sobie go odpuszczam V'(x)= 12x²−8ax−a² Teraz J pokieruj co dalej

Jerzy: Szukasz miejsc zerowych

5-latek : czyli Δ= 64a²+48x²a²

	8−√64a2+48a2x2
x1=
	24

	8+√64a2+48a2x2
x2=
	24

Mam naprawdę z tym kłopoty Nie rozwiazywalem takich zadań bardzo długo

Jerzy: Skąd w Δ masz x ?

kochanus_niepospolitus: dlaczego w Δ występuje x²

5-latek : Nie wiem kto kieruje moją ręką Δ= 64a²+48a²= 112a² √Δ= √112a²

5-latek :

	8+√112a2		1
x1=		=		+√112a2
	24		3

	8−√112a2		1
x2=		=		−√112a2
	24		3

5-latek : Zle jest

	1		√112a2
x1=		+
	3		24

	1		√112a2
x2=		−
	3		24

Jerzy: Troche poskracaj i ustal gdzie pochodna zmienia znak z + na − ?

Jerzy: 112 = 16*7

5-latek : zapisze sobie to tak √112a²=√7*16a² = 4a*√7 wiec

	1		a√7
x1=		−
	3		6

	1		a√7
x2=		+
	3		6

Jerzy: Dobra..gdzie zmiana z + na − ?

5-latek : Nie wiem .

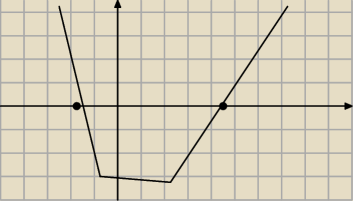
Jerzy: To naszkicuj wykres pochodnej

5-latek : a musi by dodatnie Wobec tego dla a=1 x₁= U{0,33−0,44}<0 x₂>0

5-latek :

Jerzy: Tu ,gdzie pochodna tak zmienia znak, funkcja ma maksimum lokalne i to koniec zadania

Jerzy: No i popraw m. zerowe...zjadłeś a

5-latek : Dzieki przede wszystkim za cierpliwość jak już dojde do tego dzialu to pewnie będę takie zadanka smigal

Jerzy: I teraz widze, że żle masz funkcję V ... i wszystko jest do bani ( x < 0 )

Jerzy: Wychodzi ładny wynik: x = 1/6 a

kochanus_niepospolitus: Jerzy ... co Ci w funkcji V(x) nie pasuje?

kochanus_niepospolitus: V'(x) i owszem ... ma źle ... ale V(x) jest dobrze

kochanus_niepospolitus: chodzi o post z 11:05 <−−− tu dobrze później już V(x) jest źle (pojawia się magicznie −a²x)

Jerzy: Oczywiście +a²x...i wynik końcowy jak podałem

5-latek : A niech to ..... Tyle liczenia na darmo

5-latek : V(x)=a²x−4ax²+4x³ V(x)= 4x³−4ax²+a²x V'(x)= 12x²−8ax+a² ===================== Δ= 64a²−48a²= 36a² √Δ= 6|a| ale a>0 to = 6a

	8−6a		1		1
x1=		=		−		a
	24		3		4

	1		1
x2=		+		a
	3		4

	1
jak z tego dostać		a=x
	6

Jerzy: przecież gubisz a licząc x₁ i x₂ ( już Ci to pisałem)

5-latek : czy dlatego ze a jest stale ?

	1
To wtedy x1=
	12

	14		7
a x2=		=
	24		12

Albo ja w tym momencie czegos nie lapie

Jerzy:

	−b + √Δ
x1 =		.... a ile u Ciebie wynosi b ?
	2a

kochanus_niepospolitus: jaki jest wzór na x_1,2

	−b +/−√Δ
x1,2 =
	2a

2a = 8 ok −b = +8a ... a nie +8

kochanus_niepospolitus: druga sprawa ... ile to jest 64−48

Jerzy: nawet tego nie zauważyłem

kochanus_niepospolitus: w sensie ... 2a = 24 ... ok

Jerzy: zrób sobie małolat mocną kawę ...

5-latek : b=−8a

Jerzy: czyli: − b = 8a , a u Ciebie.....8 ( bez a, bo go zgubiłeś)

Jerzy: no i ....... √Δ = 4a , a nie 6a jak u Ciebie

5-latek : Sam nie wiem dlaczego tak nieudolnie dzisiaj licze

Jerzy: nie przejmuj się, mnie się to też często zdarza

5-latek : Jerzy Już wypiłem dzisiaj 3 kawy ale i tak sen mnie dopadl (nawet jak elektryk wiercil dziekuje Wam za pomoc

5-latek : kochanus_niepospolitus Dobrze ze sledzisz rozwiązanie i wytykasz bledy

5-latek : Już jutro napisze to rozwiązanie z książki Natansona Naprostszse zadania na maksimum i minimum dzisiaj już nie mam Powera .