prosze o pomoc! marcin: Wyznacz wszystkie wartosci parametru p, dla ktorych rownanie |x²+4x|−3=p posiada co najwyzej dwa rozwiazania.

Metis: Graficznie.

marcin: Ale jakie to bedzie przeksztalcenie?

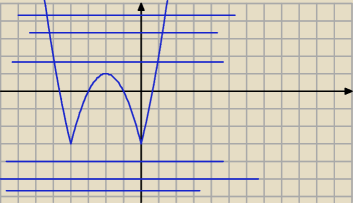
5-latek : te pozione linie to y=p

5-latek : potrafisz narysować wykres funkcji y=|x²+4x|−3 ?

PW: Albo (1) |x² + 4x| = p + 3. Lewa strona równania jest dla dowolnej x∊R liczbą nieujemną (z definicji wartości bezwzględnej). Równanie nie ma zatem rozwiązań dla p + 3 < 0, czyli dla p < − 3. Dla p = − 3 mamy do czynienia z równaniem |x² + 4x| = 0 x² + 4x = 0 x(x+4) = 0, które ma dwa rozwiązania. Dla p > − 3 równanie (1) jest równoważne alternatywie równań x² + 4x = p + 3 ∨ x² + 4x = − (p + 3) x² + 4x − (p + 3) = 0 ∨ x² + 4x + (p + 3) = 0 Pierwsze z tych równań ma dwa rozwiązania (zawsze, wyróżnik Δ = 4² + 4(p + 3) > 0). Aby alternatywa równań miała tylko dwa rozwiązania, drugie z nich musi tych rozwiązań nie mieć w ogóle, to znaczy musi być 4² − 4(p + 3) < 0, czyli 4p > 16 − 12 p > 1. Odpowiedź: Badane równanie ma co najwyżej dwa rozwiązania dla p∊<−∞,−3>∪(1,∞).

PW: Korekta: ... dla p∊(−∞,−3>∪(1,∞)

marcin: Dzieki