a Robert: Witam, mógłby mi ktoś wytłumaczyć to zdanie na jakimś przykładzie? Nie moge tego zrozumieć: ''Ponieważ przekątne równoległoboku dzielą się na połowy, z twierdzenia Talesa, odległości punktu przecięcia się przekątnych od boków równoległoboku są równe połowie odpowiednich wysokości.''

Robert: Ktoś rzuciłby swoim matematycznym okeim ? Nie daje mi to spokoju i nie moge przez to zrozumieć zadania

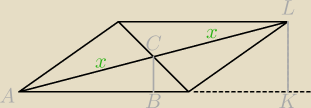
yht: CB − odległosć punktu przecięcia przekątnych równoległoboku od boku LK − wysokośc równoległoboku ponieważ AC = CL = x, to AC = x, AL = 2x oraz trójkąty ABC i AKL są podobne w skali k=2 czyli każdy bok trójkąta AKL jest 2 razy większy od odpowiadającego boku trójkąta ABC

	1
zatem musi być musi być CB =		LK
	2

Robert: Takiego wyjaśnienia potrzebowałem, baardzo dziękuje . Miłego wieczoru !

Robert: A może jeszcze dla jasności, da sie w podobny sposób ''pokazać'' jak to się ma przy drugiej wysokości? Tej opuszczonej na krótszy bok

Robert: Chyba już sam widze... ten odcinek od punktu przecięcia do boku jest pod kątem prostym, tak?

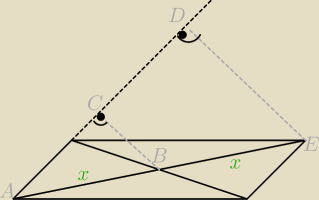
yht: dokładnie, jest pod kątem prostym

	1
trójkąty ABC i AED są podobne w skali k=2, dlatego musi być BC =		DE
	2