pole wycinka kola sagitarius: Mam prośbę. Koło dzielimy na n pasków o równej szerokości. Jak wyliczyć pole dowolnego paska?

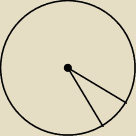
Godzio: Rozumiem, że o wycinki chodzi?

	1
P =		* πr2
	n

Godzio: Czy może o takie coś? ?

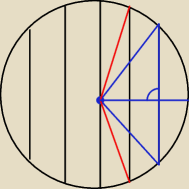
Rafal44: Załóżmy, że chcemy policzyć pole skrajnego paska. Jest ono równe różnicy pól wycinka kołowego (niebieskie promienie) i trójkąta równoramiennego (też niebieskiego). Znamy długość promienia

	2r
okręgu i szerokość pojedynczego paska (		). Z twierdzenia Pitagorasa liczymy długość
	n

podstawy niebieskiego trójkąta, potem jego pole (znamy wysokość). Korzystając z trygonometrii znajdujemy przybliżoną miarę kąta wyznaczającego niebieski wycinek kołowy. Załóżmy teraz, że chcemy policzyć pole drugiego paska od końca. Postępujemy analogicznie, z tą różnicą, że na końcu otrzymujemy pole figury złożonej z dwóch pasków. Jednakże pole jednego z nich już wcześniej poznaliśmy...

sagitarius: Chodzi dokładnie o ten drugi rysunek Godzio, tak jak rafal44 narysował. Postępowałem dokładnie trak jak pisałeś Rafal44. Jedyny problem w tym że we wzorze na pole wycinka koła występuję kąt P=(α/360)πr². Żeby go obliczyć trzeba byłoby posłużyć się funkcją arccos. Masz może inny pomysł?

daras: otwierasz tablice matematyczne i masz:

	1		1
S =		[lr−a(r−h)] =		(a−sinα)r2
	2		2

	1		πα
lub w stopniach S =		(		−sinα)r2, gdzie α−kąt środkowy, a −długość cięciwy,
	2		180

l−dług. łuku, r−promień koła

sagitarius: Owszem, to wiem. Problem w tym, żeby jakoś ominąć wyliczanie kąta. Chcę stworzyć mały programik który by to liczył podając mu tylko dwie wartości: promień okręgu i ilość odcinków na które będzie dzielony.