Geometria, trapez opisany na okręgu Nemi: Potrzebuję pomocy z ukochaną geometrią 'Dany jest trapez prostokątny opisany na okręgu o promieniu R. Jedna z podstaw jest 3 razy dłuższa od drugiej podstawy. Oblicz pole tego trapezu.'

Nemi: Podbijam :3

Rafal44: a − długość krótszej podstawy 3a − długość dłuższej podstawy h − długość wysokości opuszczonej na dłuższą podstawę h=2R Przedstaw długość ramienia nieprostopadłego do podstawy na dwa sposoby: raz z wykorzystaniem twierdzenia Pitagorasa i wysokości opuszczonej na dłuższą podstawę, drugi raz z własności okręgu wpisanego w czworokąt (sumy długości przeciwległych boków są równe). Następnie połącz równości i wyznacz a w zależności od R, na końcu podstaw do pola trapezu.

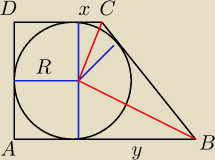
g: Oznaczam: β = kąt ABC.

R+y		β		180−β		β
	= 3 tg		= R/y tg		= 1/tg		= R/x
R+x		2		2		2

Trzeba stąd wyznaczyć x i y. Pole trapezu = 2R² + R(x+y)

Rafal44: Alternatywne rozwiązanie |AD|=h=2R |BC|=x Z własności okręgu wpisanego w czworokąt: 3a+a=x+2R x=4a−2R Z twierdzenia Pitagorasa x²=h²+(2a)²=4R²+4a² Łącząc powyższe równości: x²=(4a−2R)²=4R²+4a² 16a²−16aR+4R²=4R²+4a² 12a²=16aR 3a=4R

	4
a=		R
	3