Dziedzina funkcji pierwiastkowej 5-latek : Dla jakich wartości parametru m dziedzina funkcji f określonej wzorem f(x)= √m²+1+m²x−x² zawiera przedzial domknięty <0,4> −x²+mx²+m²+1≥0 (takie zalozenie musi być teraz rozwiazac ta nierownosc i druga −x²+m²x+m²+1 ≤4 ?

5-latek : To pewnie będzie cos takiego

5-latek : jeśli rozwiaze zalozenie to dostane Δ= m²+4m²+4 czyli Δ= 5m²+4 Teraz muszse policzyć

	−m−√5m2+4
m1=
	−2

	−m+√5m2+4
m2=
	−2

5-latek :

	−m−√5m2+4		−m+√5m2+4
czyli nasz m ∊<		,		>
	−2		−2

5-latek : Wiec teraz musze rozwiazac koniunkcje nierownosci ? czyli m₁≥0 i m₂≤4 Tak ?

5-latek :

−m−√5m2+4		m+√5m2+4
	=		i to ma być ≤4
−2		2

−m+√5m2+4		m−√5m2+4
	=		i to mam być ≥0
−2		2

Post 8:34 jest zle napisany

5-latek :

5-latek :

5-latek :

5-latek : Wk...a mnie to ze do tej pory nikt nie porafil powiedzieć czy dobre myslenie ? czy dalej tak obliczac tak jak napisałem ? Znowu to napiszse . Nie czekam na gotowe rozwiązanie bo zaczalem to rozwiazywac Jak jest zadanie banalne i nikt się nie odzywa a rozwiazan jest multum Ja tez staram się pomagać w miare swoich możliwości

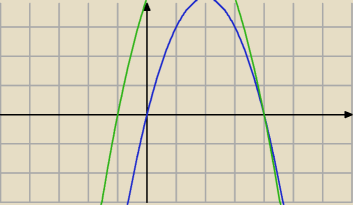
Mila: g(x)=−x²+m²x+m²+1 −x²+m²x+m²+1≥0 Δ≥0 dla m∊R W zbiorze rozwiązań nierówności ma się zawierać przedział <0,4> g(0)≥0 i g(4)≥0

5-latek : Dobry wieczor Milu Pozdrawiam czyli tak jak obliczyłem Δ=5m²+4 Ma ona być ≥0 ale 5m²+4 >0 zawsze czyli rozważaniem tej nierownosci jest zbior liczb R ten warunek Δ≥0 to dlatego ze jeśli w dziedzinie ma się zawierac ten przedzial to musza być miejsca zerowe ? teraz g(0)≥0 Dostane m²+1≥0 a to jest zawsze >0 czyli m∊R drugi warunek g(4)≥0 16+4m²+m²+1≥0 5m²+17≥0 tez wychodzi zbior R W odpowiedzi do zadania mam m∊(−∞ −√3)U(√3,∞)

5-latek :

5-latek : Co robie zle ?

Metis: Warunek Δ≥0 to z założenia, że liczba podpierwiastkowa musi być nieujemna czyli może być równa 0 i dodatnia

Metis: Aj nie doczytałem Nie o to chodzi

5-latek : Metis ja tez się dzisiaj myle

Metis: Dziedzina funkcji ma zawierać przedział <0,4>. Dziedzina : −x²+m²x+m²+1≥0 Czyli Δ>0 oraz g(0)≥0 i g(4)≥0 tak myślę

Mila: 5−latku, masz błąd. g(4)=−16+4m²+m²+1

Metis: ≥0 Zatem Δ≥0

5-latek : Już widze Ma ma być g(4)= −(4)²+m²*4+m²+1 A ja policzyłem tak g(4)= (−4)² i tak dalej dziekuje CI bardzo za okazana pomoc

Mila: W tym zadaniu Δ>0.

5-latek : Tak myslaem bo muszse by dwa miejsca zerowe