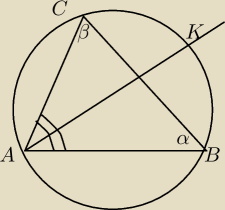
Na trójkącie ABC, w którym |BC|=a, |∡ABC|=α i |∡ACB|=β, opisano okrąg. Polaczek: Na trójkącie ABC, w którym |BC|=a, |∡ABC|=α i |∡ACB|=β, opisano okrąg. Dwusieczna kąta A przecina okrąg w punkcie K. Oblicz długość odcinka AK.

Polaczek: wydaje mi się, że trzeba wykorzystać twierdzenie sinusów, że by jakoś uzależnić nieznane długosci bokow i kąta od tych znanych.. ale coś mi nie idzie każda pomoc jest mile widziana..

Polaczek: nikt nic nie doradzi?

Eta: 1/ Łącząc punkt K a punktami B i C otrzymujemy czworokąt ABKC wpisany w okrąg zatem |∡CKB|= 180^o−2γ , to cos(180^o−2γ)= −cos2γ 2/ dwusieczna dzieli łuk CB na dwa równe łuki BK=CK to kąty wpisane parte na tych samych łukach mają równe miary ( γ 3/ z tw. kosinusów w ΔCBK wyznaczamy długość "d" a²=d²+d²+2d²cos2γ ⇒ a²=2d²(1+cos2γ) i 1+cos2γ= 2cos²γ

	a2		a
to d2=		⇒ d=
	4cos2γ		2cosγ

4/ z tw. sinusów w ΔABK:

	x		d		dsin(α+γ)
		=		⇒ x=
	sin(α+γ)		sinγ		sinγ

można ten wynik zostawić , bo mając miary kątów α i β mamy też miarę kąta γ=180^o−(α+β) lub dalej przekształcać podstawiając za γ= 180^o−(α+β): x= ....................

Polaczek: dziękuję