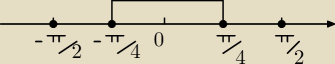matematykaszkolna.pl
#workout PrzyszlyMakler: Rozwiąż nierównośc dla x ∊ <−π; π>
 π 
|cosx|(cosx − cos
) ≥0
 4 
 π π 
D: cosx ∊ <−
;
>
 2 2 
 π 
cosx(cosx − cos
) ≥0
 4 
 π 
cosx≥0 (cosx − cos
) ≥0
 4 
 π 
x ∊ D x ≥
 4 
 π π 
x ∊ <−
;
>
 4 4 
 π π 
Odp to częśc wspólna, czyli: x ∊<−
;
>
 4 4 
Czy zapis i obliczenia i wynik są dobre?
2 kwi 23:19
ICSP: Co to w ogóle za dziedzina ?
 π π π π 
Odp : x ∊ [−
,
] ∪ {−
,
}
 4 4 2 2 
2 kwi 23:29
PrzyszlyMakler: Bo mamy moduł z cosx, a ów przyjmuje wartości dodatnie, dla −pi/ ; pi/2.
2 kwi 23:34
PrzyszlyMakler: A jeżeli odpowiedzią jest suma, to dlaczego napisałeś w ten sposób, skoro −π/4 do π/4 zawiera się w przedizale −π/2 do π/2?
2 kwi 23:36
ICSP: Czyli |cos(π)| nie istnieje czy jak ?
2 kwi 23:37
ICSP: to jest przedział do którego dorzuciłem dwie liczby. Nawiasy { , } Oznaczają zbiór.
2 kwi 23:38
PrzyszlyMakler: Nie rozumiem odpowiedzi.emotka
2 kwi 23:55
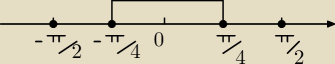
ICSP: rysunek
2 kwi 23:59
PrzyszlyMakler: Ale przecież |cosx| jest większy równy zero dla −π/2 do π/2.. Nie wiem dlaczego tylko te punkty są odpowiedzią.
3 kwi 00:26
ICSP:
 π 
ale się zeruje dla x = ±
, więc całe wyrażenie po lewej stronie się wyzeruje.
 2 
3 kwi 00:29
PrzyszlyMakler: Okej. A dlaczego w odpowiedzi nie uwzględniamy obszaru od −pi2 do −pi/4 i pi/4 do pi/2. Przecież te przedziały również są większe od 0.
3 kwi 00:34
ICSP:
 √2 
W tych przedziałach |cosx| jest dodatni ale (cosx −
) jest ujemne, więc iloczyn jest
 2 
ujemny.
3 kwi 00:39
PrzyszlyMakler: W końcu rozumiem. To zadanie wymagało ogromnej skrupulatności. Dziękuję za cierpliwość i dążenie, abym zrozumiał. Jeszcze takie małe pytanko, trzeba było wyznaczać dziedzinę? Jeżeli tak, to jaka ona jest?
3 kwi 00:41
ICSP: Na siłę możesz przyjąć za dziedzinę zbiór podany w treści zadania.
3 kwi 00:54