Optymalizacja, geometria analityczna, trójkąt pafrykk:

	1
Dana jest rodzina trójkątów ABC spełniających warunki: A=(3		;0); B=(a;0), gdzie a∊(0;4),
	2

wierzchołek C należy do paraboli o równaniu y=4x − x² oraz kąt ABC = 90^o. Wyznacz współrzędne punktu C, dla którego pole trójkąta ABC jest największe.

	7		35
Mam z tym zadankiem problem. Musi wyjść C=(		;		).
	3		9

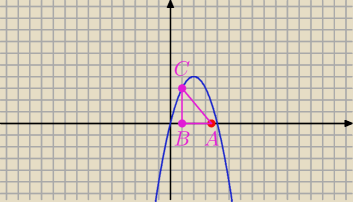Janek191: P_Δ = 0,5 I 3,5 − a I*( 4 a − a²} ; dla a < 3,5 mamy P_Δ = 0,5*(3,5 − a)*( 4 a − a²) = (3,5 − a)*( 2 a − 0,5 a²) P '(a) = − 1*( 2 a − 0, 5 a²) + ( 3,5 − a)*( 2 − a) = −2 a + 0,5 a² +7 −3,5 a − 2 a + a² = = 1,5 a² − 7,5 a + 7 = 0