geometria rafal: Dany jest czworokąt wypukły ABCD niebędący równoległobokiem. Punkty M, N są odpowiednio środkami boków AB i CD. Punkty P,Q są odpowiednio środkami przekątnych AC i BD. Uzasadnij, zę jeżeli odcinki MN i PQ są prostopadłe, to |AD| = |BC|.

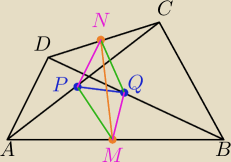
Rafal44: Prosta MQ dzieli odcinki AB i DB na dwie równe części, a zatem z twierdzenia odwrotnego do twierdzenia Talesa wynika, że prosta MQ jest równoległa do prostej AD. Ponadto, na mocy

	AD
podobieństwa trójkątów MBQ i ABD w skali 1:2, MQ=		. Analogicznie dowodzimy:
	2

	AD		BC		BC
NP||AD i NP=		=MQ, MP||BC i MP=		, NQ||BC i NQ=		=MP. Wobec tego
	2		2		2

czworokąt MQNP jest równoległobokiem. W myśl założeń, jego przekątne przecinają się pod kątem

	AD		BC
prostym, co implikuje, że jest on także rombem i		=MQ=NQ=		, czyli AD=BC. To
	2		2

kończy rozwiązanie zadania.