Współrzędne punktu C Koq12: Dane są punkty A=(1,3) B = (4,5). Wyznacz współrzędne takiego punktu C należącego do prostej y=7, by liczba d=|AC| + |CB| była najmniejsza.

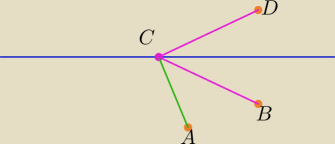
Rafal44: Niech D=(4,9) będzie punktem symetrycznym do punktu B=(4,5) względem prostej y=7. Z własności symetrii |AC|+|BC|=|AC|+|DC|. Suma |AC|+|DC| jest najmniejsza, gdy punkt C leży na prostej |AD|. Liczymy równanie prostej y=ax+b przechodzącej przez punkty A i D. 3=a+b 5=4a+b

	2
a=
	3

	7
b=
	3

	2		7
Szukamy punktu wspólnego prostej y=		x+		z prostą y=7.
	3		3

	2		7
7=		x+		/*3
	3		3

21=2x+7 2x=14 x=7 C=(7,7)

Rafal44: Przepraszam, napisałem straszne bzdury − zamiast punktu D podstawiłem punkt B. W ogóle nie patrzcie na tamte rachunki. Liczymy równanie prostej y=ax+b przechodzącej przez punkty A i D. 3=a+b 9=4a+b a=2 b=1 Szukamy punktu wspólnego prostej y=2x+1 z prostą y=7. 2x+1=7 x=3 C=(3,7)