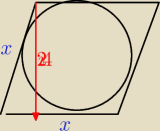
planimetria Karolcia: Cosinus jednego z kątów romby jest równy −1/3, a promień okregu wpisanego w ten romb jest równy 12. Oblicz pole rombu cos −1/3 jest dla kąta rozwartego i nie wiem teraz co dalej z tym zrobić czyli kąt ma cos(90+α)=−1/3

dero2005:

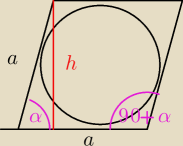
	1
cos(90+α) = cos90*cosα − sin90*sinα = −
	3

	1
0− 1* sinα = −
	3

	1
sinα =
	3

h		1
	= sinα =
a		3

a = 72 P = a²sinα =

Karolcia: 72*72:3=1728 ale coś tu sie nie zgadza bo nie ma do wyboru takiej odpowiedzi

dero2005: a jakie są możliwości?

Karolcia:

	432√2
48 albo 432√2 lub 216√2 i
	3

dero2005: już wiem gdzie jest nieprawidłowość, ten kąt po lewej stronie, który oznaczyłem jako w rzeczywistości jest równy 90−α

Karolcia: dobrze dziękuję

dero2005: wychodzi 432√2

Karolcia: A jak to wyliczyles? Probuje ale mi nie wychodzi

dero2005: Jak pisałem 19:56 ten kąt ostry to jest 90−α Wcześniej policzyłem, że sinα = ¹₃

	2√2
Stąd cosα = √1−sin2α =
	3

	2√2
sin(90−α) = cosα =
	3

h		2√2
	= sin(90−α) =
a		3

a = 18√2

	2√2
P= a2*sin(90−α) = (18√2)2*		= 432√2
	3