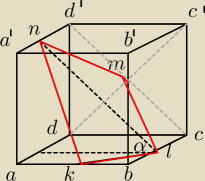
pole płaszczyzny kl5: W sześcianie abcda'b'c'd' wyznaczono punkty klmn, które są odpowiednio środkami krawędzi ab,bc,cd' i a'd'. Długość krawędzi sześcianu jest równa a. Oblicz pole czworokąta klmn oraz tangens kąta nachylenia płaszczyzny klmn do płaszczyzny podstawy sześcianu. Czy może ktoś sprawdzić mi to zadanie? Otrzymałem:

	√2
|KL|=		a
	2

	√6
|NK| =		a
	2

	√3
|NM|=|ML|=		a
	2

|NL|=a√2

	√3
PKNL=		a2
	4

	3
PNB'L=		a2
	8

	3+2√3
P=		a2
	8

α=45^o tg 45^o=1 Z góry dzięki za pomoc.

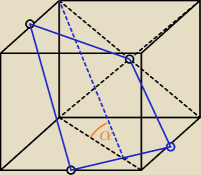dero2005: czy te proste leżą w jednej płaszczyźnie?

Matej:

	2√2
no na Twoim rys wydaje mi się, że tak. czyli tg =		a ?
	3

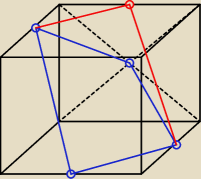dero2005: a na tym rysunku niebieski czworobok jest w tej samej płaszczyźnie co czerwony?

kl5: Nie

dero2005: ale przecież dwa boki czworoboków pokrywają się (kl i kn) to dlaczego mówimy o płaszczyźnie klmn?

kl5: Tak, mój błąd. Słabą jakość treści zadania mam i punkt m jest na środku krawędzi C'D' a CD', Dzięki za wychwycenie błędu

kl5: * a nie CD'.

dero2005: