Wykaż że Senea: Dany jest prostokąt ABCD. Na boku CD wybrano taki punkt E, że |DE| = 4*|CE| . Przekątna AC przecina się z prostą BE w punkcie F. Wykaż, że stosunek pola czworokąta AFED do pola trójkąta CDF wynosi 19/4 .

Senea: Jeżeli nie możecie tego udowodnić to proszę napiszcie. Może pomyliłam się z tym stosunkiem pól.

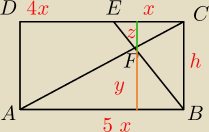
Senea: z−wysokość ΔFEC y−wysokość ΔABF Próbowałam to zrobić tak. Przyjęłam, żę trójkąt EFC jest podobny do trójkąta FAB czyli

5x		y		1
	=		czyli 5z=y. Z tego wynika, że 6z=h czyli z=		h.
x		z		6

	x*h
PΔBCE=
	2

	(4x+5x)*h
P ABED=
	2

	h*x
PΔFCE=
	12

	25*x*h
PΔABF=
	12

Później odejmuje te pola żeby otrzymać Pola które muszę wyliczyć w zadaniu ale nie wychodzi mi ten wynik.

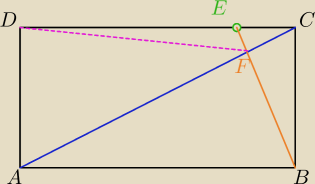
===: wychodzi 24/5

Senea: Dzięki za odpowiedź. Mogłabyś mi powiedzieć jak to robiłaś? Bo mi tam wychodzi 29/5 i nie wiem gdzie popełniłam błąd.

Eta: Ja też mam

	29
Odp :
	5

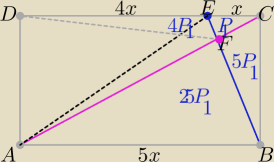
Eta: P(ADEF)= 30P₁−P₁=29P₁ , P(DFC)= 5P₁

	29P1		29
to: ....=		=
	5P1		5

===: chyba jednak "skopałem" Jeśli pole prostokąta ABCD przyjmiemy za X to:

	1		1		1		1
pole ΔCEF=		*		*		X=		X
	2		5		6		60

	1		1		29
pole czworokąta AFED=		X−		X=		X
	2		60		60

	1		1		1
pole ΔCDF=		*1*		X=		X
	2		6		12

29		1		29
	X:		X=
60		12		5

Eta: A ja wciąż "kocham" trapezy

Senea: Dzięki wielkie wszystkim Chyba nam na maturze prima aprilis zrobili :'D

Eta: