Funkcja homograficzna Qwerty: Coś mi nie wychodzi wykres, proszę o pomoc i rozpisanie kolejnych kroków F(x)=^|x|_x−1

kochanus_niepospolitus:

	1
a Ty napisz funkcję korzystając z U a nie u do zapisu ułamku (		a nie 1√2) bo
	√2

tutaj nic nie widać

Qwerty:

	|x|
F(x)=
	x−1

Czy teraz pasuje?

kochanus_niepospolitus: tak ... teraz pasuje 0) D_f = R/{1} przypadek 1) x≥0 i x≠1

	x		x−1 +1		1
F(x) =		=		= 1 +
	x−1		x−1		x−1

	1
czyli F(x) to będzie funkcja g(x) =		przesunięta o jaki wektor
	x

przypadek 2) x<0

	−x		1
F(x) =		= −		− 1
	x−1		x−1

	1
czyli F(x) to będzie funkcja g(x) = −		przesunięta o jaki wektor
	x

Qwerty: 1) [1,1] 2) [−1,−1] Nie da się tego jakoś prościej? Na lekcji robiliśmy tak ze wykres z prawej strony odbijalismy na lewą za sprawą wartości bezwzględnej

kochanus_niepospolitus: zależy od postaci funkcji 'obijać' możesz jeżeli: 1) D_f jest symetryczna względem osi OY (a nie jest ) 2) funkcja jest parzysta/nieparzysta ... a nie jest ze względu na D_f

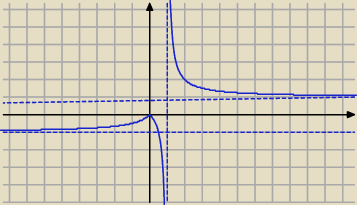
kochanus_niepospolitus: widzisz jaki śliczny wykres wychodzi Pokaż mi jak Ty chciałeś cokolwiek odbijać Jedyne 'odbicie' byłoby dla Ciebie nielogiczne ... więc nawet lepiej o tym nie wspominać

Qwerty: Co to znaczy D symetryczna względem osi OY?

kochanus_niepospolitus: to znaczy, że np. D_f = R/{−2,2} a nie D_f = R/{−2,1}

Qwerty:

	−2|x|−1
A w takiej f(x)=
	|x|+2

Jaka jest dziedzina? Tylko −2? Wiem że w tej funkcji będzie odbicie

kochanus_niepospolitus: D_f = R ... przecież mianownik > 0 dla dowolnego x

Qwerty: Faktycznie, to za każdym razem gdy w mianowniku będzie wartość bezwzględna można odbić wykres?

Qwerty: To gdyby w pierwszej funkcji wyszła dziedzina R−{1,−1} to wtedy moge odbić? Ale gdy jest tylko jedna liczna to nie można odbijać?