Jakie są długości boków powstałego trójkąta? Anon: Na trójkącie ABC o bokach długośc iAB|=9, |AC|=3 i |BC|=7 opisano okrąg. W punkcie A poprowadzono styczną do okręgu, która przecięła przedłużenie boku BC trójkąta w punkcie D. Oblicz długości boków trójkąta ACD. Wykorzystaj informację że kąt |DAC|=|ABC|. To zadanie już się pojawiło na forum 273897.html, jednak nie zostało ono wyjaśnione, a link podany w jednej z odpowiedzi nie działa.

Mila: Masz jakąś odpowiedź do zadania, bo mam dziwne wyniki.

Anon: AD = 21/8 DC = 7/8

Mila: Liczę jeszcze raz.

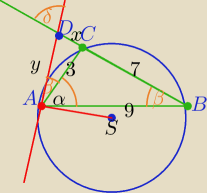
Mila: Korzystając z podanej informacji: ΔACD∼ΔADB cecha kkk, |∡DAC|=|∡ABC|,∡ADC kąt wspólny dla obu trójkątów, ∡DCA=α+β

x		y
	=
y		x+7

y²=x*(x+7) Teraz oblicz cosβ z tw.cosinusów w ΔABC . Następnie zastosuj tw. cosinusów w ΔACD. Jak nie wyjdzie , to napiszę.

Mila: albo tak (łatwiej): W ΔABC: 9²=3²+7²−2*3*7 *cos(∡ C)

	23
cos(∡C)=−		kąt rozwarty
	42

	23
cos(180−∡C)=
	42

W ΔACD:

	23
y2=x2+32−2*3x*
	42

	23
y2=x2+9−		x
	7

	23
x*(x+7)=x2+9−		x
	7

	23
x2+7x=x2+9−		x
	7

	23
7x+		x=9
	7

72		7
	x=9 /*
7		72

	9*7
x=
	72

	7
x=
	8

	7		7
y2=		*(		+7)
	8		8

	49		49
y2=		+
	64		8

	49		392
y2=		+
	64		64

	441
y2=
	64

	21
y=
	8

odp.

	7
|DC|=
	8

	21
|AD|=
	8

Anon: Ślicznie dziękuję za rozwiązanie. 2 dni nad tym spędziłem i na nic mądrego nie wpadłem. Nie ma to jak wprawiony umysł

Mila: