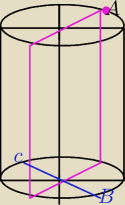
 Przez dowolny punkt A okręgu górnej podstawy walca poprowadzono przekrój płaszczyzną
zawierającą oś walca. W dolnej podstawie walca poprowadzono średnicę BC, prostopadłą od
przekroju osiowego. Wiedząc, że promień podstawy walca jest równy r oraz |∡ BAC|= α,
α ∊(0,90◯), oblicz wysokość walca.
Przez dowolny punkt A okręgu górnej podstawy walca poprowadzono przekrój płaszczyzną
zawierającą oś walca. W dolnej podstawie walca poprowadzono średnicę BC, prostopadłą od
przekroju osiowego. Wiedząc, że promień podstawy walca jest równy r oraz |∡ BAC|= α,
α ∊(0,90◯), oblicz wysokość walca.
| α | ||
więc: |∡ BAO|= | (gdzie O −−− środek podstawy walca) | |
| 2 |
| α | |BO| = r | α | ||||
teraz z trygonometrii: tg | = | czyli |AO| = r*ctg | ||||
| 2 | |AO| | 2 |