analiza matematyczna hope: wyznacz punkt, w którym styczna do paraboli y=x² jest nachylona do osi x pod kątem 60*

hope: up

kochanus_niepospolitus: nachylenie stycznej = a = tgα tg 60^o = ... = a = f'(x₀) = 2x₀ −> x₀ = ...

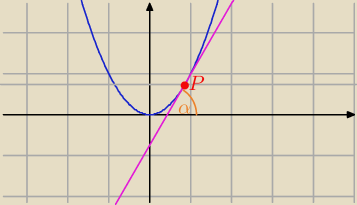
Mila: α=60^o P=(x₀,y₀) − punkt styczności z wykresem f(x) f(x)=x² f'(x)=2x s: y =ax+b a=f'(x₀) , a=tg60^o=√3 f'(x₀)=2*x₀ 2*x₀=√3

	√3
x0=
	2

	√3		√3		3
f(		)=(		)2=
	2		2		4

Możesz napisać równanie stycznej

	3		√3		3
s: y=√3*x+b ,		=√3*		+b⇔b=−
	4		2		4

	3
s: y=√3x−
	4

===============

Mila:

	√3		3
P=(		,		) − punkt styczności.
	2		4

bodzan: αβγδΔπΩ∞

mkaminski: dasdsadsdsaaasd