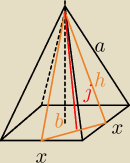
 A więc, z tw Pitagorasa h=√a2−x24
b=x√22
z tego by wynikało że j=√a2−3x24
I P(x)= x√24*√a2 − 3x24 I pytanie co dalej
A więc, z tw Pitagorasa h=√a2−x24
b=x√22
z tego by wynikało że j=√a2−3x24
I P(x)= x√24*√a2 − 3x24 I pytanie co dalej 
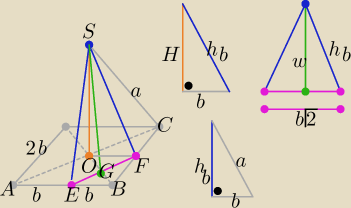 |AB|=2b , |SC|=a , |ES|=FS|=hb , |OS|=H , |EF|=0,5|AC|=b√2 , |OF|=b , |SG|=w
|AB|=2b , |SC|=a , |ES|=FS|=hb , |OS|=H , |EF|=0,5|AC|=b√2 , |OF|=b , |SG|=w
| b√2 | 2a2−3b2 | |||
hb2=a2−b2 i w2=hb2−( | )2 ⇒ w2=..... = | |||
| 2 | 2 |
| √2a2−3b2 | ||
w= | ||
| √2 |
| 1 | √2a2−3b2 | |||
P(EFS)= P(b)= | *b√2* | |||
| 2 | √2 |
| 1 | ||
P(b)= | b√2a2−3b2 | |
| 2 |
| 3b2 | ||
P'(b)= 0,5( √2a2−3b2− | ) | |
| √2a2−3b2 |
| a2 | ||
P'(b)=0 ⇒ 2a2−3b2−3b2=0 ⇒ b2= | ||
| 3 |
| a2 | ||
dla b2= | −−− pole jest max | |
| 3 |
| a√3 | 4a2 | |||
H2=hb2−b2 ⇒ ............. H = | i Pp= 4b2= | |||
| 3 | 3 |
| 4a3√3 | ||
to V = .................. = | [j3] | |
| 27 |

 Z x zamiast x2 wszytko pięknie wychodzi
Z x zamiast x2 wszytko pięknie wychodzi 