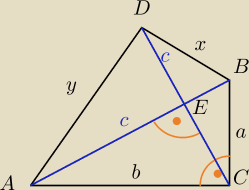
Wyraź długości x i y za pomocą a i b. Rar: W trójkącie prostokątnym ABC z kątem prostym przy wierzchołku C narysowano odcinek CD o długości |AB| prostopadły do AB. Długości odcinków |BC|=a |AC|=b |AB|=c |BD|=x |AD|=y Wyraź długości x i y za pomocą a i b.

Rafal44:

	ef
Pole S dowolnego czworokąta: S=		*sinγ, gdzie e i f to długości przekątnych, a γ to kąt
	2

ostry zawarty między przekątnymi e i f. Niech m oznacza długość odcinka DE. Pole czworokąta

	ab
ACBD możemy przedstawić na dwa sposoby: jako sumę pól trójkątów ACB (		) i ABD
	2

	cm
(		) lub korzystając z powyższego wzoru.
	2

c2		ab		cm
	=		+
2		2		2

c²=ab+cm

	c2−ab
m=
	c

Niech h oznacza długość odcinka EC, p − długość odcinka AE, q − długość odcinka BE. Pole trójkąta ACB możemy przedstawić na dwa sposoby:

	ab		ch
[ACB]=		=
	2		2

ab=ch

	ab
h=
	c

W trójkącie AEC: p²+h²=b²

	a2b2		b2c2
p2+		=b2=
	c2		c2

	b2c2−a2b2
p2=
	c2

W trójkącie BEC: q²+h²=a²

	a2b2		a2c2
q2+		=a2=
	c2		c2

	a2c2−a2b2
q2=
	c2

Pozostaje tylko zastosować twierdzenie Pitagorasa dla trójkątów AED i BED... Oczywiście, mogłem się pomylić w rachunkach, jak to ja.