Napisz wzór funkcji kwadratowej f w postaci kanonicznej Fieaore: Zbiorem wartości funkcji kwadratowej f jest przedział (−∞;8), a jednym z jej miejsc zerowych jest liczba 1. Osią symetrii wykresu funkcji f jest prosta o równaniu x=3. Napisz wzór funkcji kwadratowej f w postaci kanonicznej. To dla mnie bardzo ważne i dziękuję z góry za pomoc!

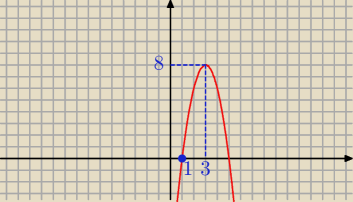
Janek191: ZW = ( − ∞ , 8 > ⇒ q = 8 Oś wykresu ma równanie x = 3 , więc p = 3 x₁ = 3 więc f( 1) = 0 zatem f(x) = a*(x − p)² + q = a*( x − 3)² + 8 oraz f(1) = 0 czyli 0 = a*( 1 − 3)² + 8 = a*4 + 8 = 4 a + 8 4a = − 8 a = − 2 Odp. f(x) = − 2*( x − 3)² + 8 ======================== Patrz też na wykres:

Janek191: W III wierszu powinno być x₁ = 1 więc f(1) = 0

wredulus_pospolitus: 1) skoro zbiorem wartości jest przedział (−∞,8) to a<0 (ramiona skierowane do dołu) 2) skoro zbiorem wartości jest przedział (−∞,8) to y_w = 8 3) skoro jednym z miejsc zerowych jest x=1 to f(1) = 0 4) skoro osią symetrii jest prosta x=3, to x_w = 3 5) skoro osią symetrii jest prosta x=3 a jednym z miejsc zerowych jest x=1 to drugim miejscem

	1+x2
zerowym będzie x=5 (ponieważ:		= 3 ⇔ x2 = 5)
	2

6) znamy współrzędne wierzchołka (punkt 2 i 4) f(3) = 8 7) postać kanoniczna funkcji kwadratowej: f(x) = a(x−x_w)² + y_w Zatem: f(x) = a(x−3)² + 8 z punktu (3) wiemy, że f(1) = 0 ... zatem: 0 = a(1−3)² + 8 ⇔ 0 = 4a + 8 ⇔ a=−2 Ostatecznie: f(x) = −2(x−3)² + 8