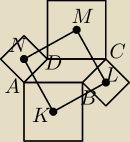
na bokach równoległoboku ABCD OM#62;: Na bokach równoległoboku ABCD zbudowano 4 kwadraty, ich środki nazwano K, L, M, N. a) Udowodnij, że czworokąt KLMN jest kwadratem. b) Udowodnij, że pole kwadratu KLMN jest równe polu równoległoboku ABCD powiększonemu o jedną czwartą sumy pól czterech kwadratów zbudowanych na bokach równoległoboku.

Mila: Jutro

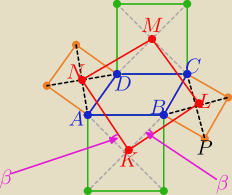Eta: Zauważ 4 trójkąty przystające : AKN i KBL i CLM i DNM z cechy (bkb) bo: AK=BK=CM=MD i AN=ND=CL=BL ( o długości połowy przekątnych kwadratów) oraz miary kątów KAB=NAD= LBP= BCL=45^o ....... zatem miary kątów rozwartych w tych trójkątach są równe 45^o+45^o +α = 90^o+α , α−−kąt ostry równoległoboku zatem czworokąt KLMN ma boki równej długości czyli jest rombem teraz należy wykazać ,że ma on kąty proste ( to będzie kwadratem) miary kątów AKN i BKL są równe ( z tego ,że trójkąty AKN i BKL są przystające β to |<NKL|=90^o zatem czworokąt (romb) KLMN jest kwadratem c.n.w

	a√2		b√2
b) |<KAN|=90o+α , |AK|=		, |AN|=		,
	2		2

gdzie a, b −−dł. boków równoległoboku i jednocześnie długości boków dobudowanych kwadratów x−−− dł. boku kwadratu KLMN to P(KLMN)= x² zaś P(ABCD)= a*b*sinα −−− pole równoległoboku z tw. kosinusów w ΔKAN x²=|AK|²+|AN|²−2|AK|*|AN|*cos(90^o+α) , cos (90^o+α)= −sinα

	a2		b2
x2=		+		+absinα
	2		2

	a2+b2		1
zatem P=		+P =		(2a2+2b2)+P(ABCD)
	2		4

c.n.u A teraz pora do.............

Eta: A tyle się po nocy naliczyłam i co? ............. Właśnie dlatego dzisiaj nie pomagam mam to w ............

olekturbo:

Mila: Tak to jest Eto. Tylko nieliczni dziękują nam. Ja mam często to samo. Obiecuję sobie, że drugi raz nie będę pomagać, ale zapominam ciągle.

Eta: Hej Mila Ktoś kiedyś powiedział na tym forum ,że ....... "za dobre towarzystwo w kawiarni nie dolicza się dodatkowych opłat do rachunku za kawę"

Mila: