Dany jest ostrosłup prawidłowy trójkątny. Krawędź podstawy ma a, a kąt łączący k Asia:): Dany jest ostrosłup prawidłowy trójkątny. Krawędź podstawy ma a, a kąt łączący krawędź ściany bocznej z krawędzią podstawy wynosi alfa. Oblicz objętość Wywnioskowałam, że wysokość spada na wysokość tego równobocznego w podstawie i dzieli ją na 2/3 i 1/3. Ta ściana jest dizelona na dwa trójkąty prostokątne przez wysokość i ma kąty (prosty, alfa, 90−alfa) W podstawie można wyliczyć wysokość podstawy z trójkąta 30 60 90. Co dalej? nie mam pomysłu na to.

Asia:): Ktoś pomoże mi? Tylko naprowadzi

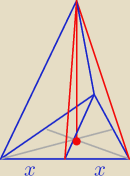Janek191: Mamy x = 0,5 a

hb
	= tg α ⇒ hb = 0,5 a*tg α
0, 5 a

	√3
hp = a
	2

	1		1
y =		hp =		a √3
	3		6

oraz h² + y² = (h_b)²

	1
h2 = 0,25 a2 tg2 α −		a2
	12

zatem

	1		1		a2√3
V =		Pp*h =		*		*√0,25 tg2 α − 112*a
	3		3		4

Janek191: h_b − wysokość ściany bocznej h_p − wysokość Δ równobocznego o boku długości a h − wysokość ostrosłupa P_p − pole podstawy ostrosłupa

Janek191: I co ?