Na jakie długości dzieli bok OM#62;: Na jakie długości dzieli bok o długości 4 w trójkącie egipskim dwusieczna kąta między bokami o długości 3 i 5?

Mila: Twierdzenie o dwusiecznej kąta w trójkącie znane?

5		3
	=		⇔3x=5y
x		y

x+y=4 −−−−−−−−

	3
y=		x
	5

	3
x+		x=4
	5

8
	x=4
5

	5
x=4*
	8

	5
x=
	2

	3
y=
	2

======

Mila: https://matematykaszkolna.pl/strona/498.html

OM#62;: Faktycznie... dziękuję po raz drugi

PW: Oznaczmy kąt między bokami o długości 3 i 5 symbolem 2α.

	sin2α		2sinαcosα		2tgα
tg2α =		=		=
	cos2α		cos2α − sin2α		1 − tg2α

	4
U nas tg2α =		, mamy więc:
	3

	4		2tgα
(1)		=		.
	3		1 − tg2α

Dla krótkości zapisu oznaczmy tgα = t > 0, równanie (1) przyjmuje postać

	4		2t
		=		, t > 0
	3		1 − t2

4 − 4t² = 6t 2t² + 3t − 2 = 0

	−3+5		1
Δ = 9 + 16 = 25, √Δ = 5. Dodatnim rozwiązaniem jest t =		=		.
	4		2

	1
tgα =		,
	2

zatem

	y		1
		=
	3		2

	3
y =		.
	2

PW: Jak zwykle skomplikowałem (udawałem, że nie znam tw. o dwusiecznej), dobrze chociaż że zgodnie zeznajemy.

Mila: Wskazówka dla uczniów− warto znać tw. o dwusiecznej.

Eta: To ja już nie piszę..............

Mila: Napisz Eto, ale innym sposobem. Coś dorysuj.

PW: Jeżeli wymyśliłaś inne rozwiązanie, to pisz Dla mnie cenną rzeczą jest różnorodność.

Mila: Ja piszę.

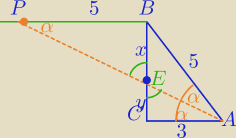Mila: ΔPBA− Δrównoramienny ΔACE∼ΔPBE⇔

x		y
	=
5		3

3x=5y i x+y=4 dalej wiadomo. ============

PW: O, i to jest piękne rozwiązanie Coś dorysować, coś zauważyć, tak jak robili starożytni.