Pochodne i optymalizacja loloo: Wyznacz długości boków prostokąta o przekątnej długości 10 tak, aby jego pole było największa podaj wartości tego pola. Może ktoś przedstawić mi przejrzyste rozwiązanie.

Janek191: Było już dzisiaj

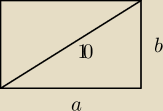
kochanus_niepospolitus: założenia: 0<a<10 0<b<10 z tw. Pitagorasa wiemy, że: a² + b² = 10² −> b² = 100 − a² −> b = √100 − a² P_p = a*b = a*√100 − a² Szukamy maksimum tegoż pola ... w tym celu należy policzyć POCHODNĄ

	−2a		100 − a2		a2
Pp' = √100 − a2 + a*		=		−		=
	2√100−a2		√100 − a2		√100−a2

	100 − 2a2
=
	√100 − a2

dla dowolnego a∊(0,10) zachodzi √100 − a² > 0 ... a więc P_p' = 0 ⇔ 100 − 2a² = 0 100 − 2a² = 0 ⇔ a² = 50 ⇔ a = 5√2 (i jest to maksimum −−− sprawdź) jeżeli a = 5√2 to: b² = 100 − a² = 100 − (5√2)² = 100 − 50 = 50 ⇔ b = 5√2 czyli ostatecznie otrzymujemy kwadrat ponieważ a=b=5√2 Na przyszłość ... kwadrat będzie ZAWSZE prostokątem o największym polu (przy zadanym warunku co do obwodu czy też przekątnej).

loloo: Można przedstawić b=10−a ? i drugie pytanie jak policzyć pochodną pierwiastka?

kochanus_niepospolitus: a w życiu to co ... a = 5 i b = 5 zbuduj mi trójkąt o bokach a=5, b=5 i przekątna = 10 pochodna pierwiastka? Odsyłam do teorii: https://matematykaszkolna.pl/strona/3420.html

loloo:

	−2a
Chodzi mi o to, że nie wiem skąd a*
	2√100−a2