pole
OM#62;:

Jakie jest pole zielonego kwadratu?
29 mar 20:47
g: | | 3 | | 4 | | 25−9−12 | | 4 | |
Bok zielonego kwadratu = √32+42 − 3* |
| − 3* |
| = |
| = |
| |
| | 5 | | 5 | | 5 | | 5 | |
29 mar 21:08
OM#62;: Możesz wytłumaczyć ?
29 mar 21:10
Gaunt: Można policzyć z pitagorasa, że długość boku tego krzyża to 5.
Boki krzyża to równoległoboki, liczę pole jednego z nich:
P=ah a=1, h
1=4
P=4
Teraz liczę pole przez drugą podstawę, czyli b=5, h
2=?
gdzie h
2 będzie długością zielonego kwadratu
h
2*b=P
29 mar 21:23
Gaunt: Teraz ja mam pytanie:
zanim g dodał rozwiązanie miałam pomysł, aby policzyć pole krzyża odejmując pole kwadratu
o boku 4 od pola kwadratu o boku 3.
Kwadrat o boku 3 powstał w wyniku połączenia czterech Δ przystających (tych powstałych po
odcięciu krzyża)
Czy dobrze myślę,że te Δ są przystające?
29 mar 22:02
Mila:
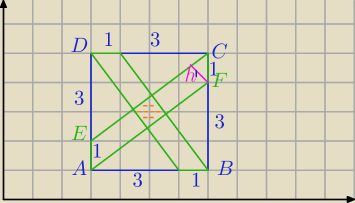
Bardzo dobrze
Gaunt
|EC|
2=3*2+4
2
|EC|=5
Równoległobok AFCE ma boki o długości: 1,5
Jedna z wysokości h=4
P
▱=1*4
4=5*h'
===========
29 mar 22:07
29 mar 22:11
Gaunt:
Milu, odpowiesz mi proszę na pytanie z 22:02?
29 mar 22:13
Mila:
Też myślałam o sposobie z zastosowaniu równoważności pól.
Te małe Δ nie są równoramienne.
Są przystające .
Możesz je połączyć np. po dwa − będą dwa deltoidy.
Marudziłam, bo jestem trochę niegrzeczną osobą i mąż mnie wyciągnął na papieroska.
29 mar 22:34
Gaunt: To można wybaczyć

Dziękuję
Milu i życzę dobrej nocy
29 mar 22:45
Mila:
Wzajemnie.

29 mar 23:21
 Jakie jest pole zielonego kwadratu?
Jakie jest pole zielonego kwadratu?
 Bardzo dobrze Gaunt
|EC|2=3*2+42
|EC|=5
Równoległobok AFCE ma boki o długości: 1,5
Jedna z wysokości h=4
P▱=1*4
4=5*h'
Bardzo dobrze Gaunt
|EC|2=3*2+42
|EC|=5
Równoległobok AFCE ma boki o długości: 1,5
Jedna z wysokości h=4
P▱=1*4
4=5*h'
 Dziękuję Milu i życzę dobrej nocy
Dziękuję Milu i życzę dobrej nocy
