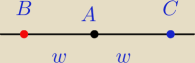
:) rumak: Mam kilka zadań w których mam podane równanie prostej, współrzędne punktu A na danej prostej oraz odległość w w jakiej mają znajdować się 2 pozostałe współliniowe punkty B C od danego punktu. Jak mogę wyliczyć ich współrzędne?

Janek191: Równanie okręgu o środku A i promieniu r = w i równanie prostej układ

rumak: Dzięki za pomoc. NIesety nie wyszedł mi dobry wynik i w razie czego napisze.

rumak: oczywiście chciałem napisać, że przeliczę jeszcze raz.... i w razie czego napiszę

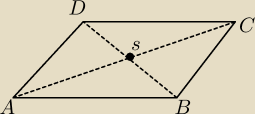
rumak: Nadal nie wychodzi mi to.. liczę zadanie http://www.zadania.info/d89/5403891 A(−3,2), C(9,6)

	9−2		6+2
S(		,		) = (3,4)
	2		2

	1
|AC| = √160 −> r =		|AC|=√40
	2

równanie okręgu: (x−3)² + (y−4)² = 40

	1
AC: (y−2)(9+3)−(6−2)(x+3) .... y =		x+3
	3

DB: y = −3x + b, podstawiam wsp. S, wychodzi y = −3x + 13 Wolfram rozwiązuje układ (x−3)² + (y−4)² = 40 y = −3x + 13 podając odpowiedzi (1,10), (5,−2), a odpowiedzi to (4,1), (2,7) Będę wdzięczny za pomoc

rumak: Nadal aktualne

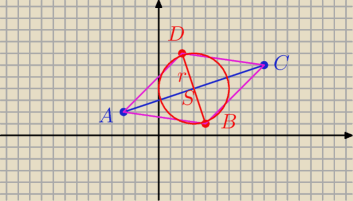
Janek191: S = ( 3, 4) I AC I = 4 √10 Pole P = 0,5 IACI*I BD I = 40 0,5*4√10 = 40 ⇒ I BD I = 2√10 więc I BS I = √10 Równanie okręgu ( x − 3)² + ( y − 4)² = 10 Prosta AC

	6 − 2		1
y =		x + b =		x + b
	9 − (−3)		3

C = ( 9, 6) więc

	1
6 =		*9 + b ⇒ b = 3
	3

	1
y =		x + 3
	3

============= Prosta BD y = −3 x + k i S = ( 3, 4) więc 4 = −3*3 + k ⇒ k = 13 y = −3 x + 13 ========= Rozwiązujemy układ równań : (x − 3)² + ( y − 4)² = 10 y = − 3 x + 13 −−−−−−−−−−−− ( x − 3)² + ( − 3 x + 13 − 4)² = 10 x² − 6 x + 9 + 9 x² − 54 x + 81 = 10 10 x² − 60 x + 80 = 0 / : 10 x² − 6 x + 8 = 0 Δ = 4

	6 − 2
x =		= 2 lub x = 4
	2

więc y = −3*2 + 13 = 7 lub y = 1 Odp. B = ( 4, 1) D = ( 2, 7) ======================

Eta:

	9−3		6+2
S(		,		)= (3,4)
	2		2

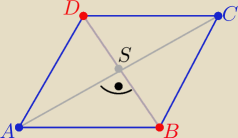
	4−2		1
Prosta AS ⊥BS to aAS=		=		to aBS= −3
	3+3		3

prosta BS : y= −3(x−3)+4 ⇒ BS: y= −3x+13 B∊BS ⇒ B(x, −3x+13)

	1
P(ABS)=		P(rombu)= 10
	4

→ → SA=[6,2] , SB=[3−x, 4−y]= [3−x, 3x−9]

	1
P(ABS)=		|d(SA,SB)|
	2

to |18x−54−6+2x|=20 ⇒ |20x−60|=20 ⇒ |x−3|=1 ⇒ x=4 lub x=2 to y= −12+13=1 lub y=−6+13=7 B(4,1) D(2,7)

Eta:

Janek191: A Rumak: gdzieś galopuje

Eta: Zanim przejrzy Twojego "tasiemca" to mu się trochę zejdzie