Trapez równoramienny OM#62;: W trapezie równoramiennym ABCD podstawy mają długości: |AB| = 10, |CD|=4 natomiast ramiona |BC|=|DA|=5. a) Na trapezie ABCD da się opisać okrąg. Środek tego okręgu leży na prostej przechodzącej przez środki obu podstaw w odległości x poniżej dolnej podstawy. Oblicz x, a następnie promień okręgu opisanego. b) Przedłużenia ramion BC i AD spotykają się w punkcie F, tworząc trójkąt równoramienny ABF. Udowodnij, że pole tego trójkąta mieści się 3 razy w polu kwadratu o boku 10. Proszę o podpowiedzi

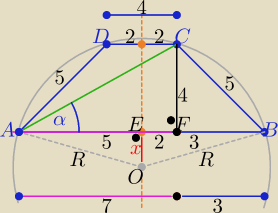
Eta: a) w trójkącie AFC |AC|=√7²+4²=√65 sinα= U{4}{√65

	5		5√65
z tw. sinusów w ΔABC :		=2R ⇒ R=
	sinα		8

	5
w ΔAOE : x2=R2−52 ⇒ x=....... =
	8

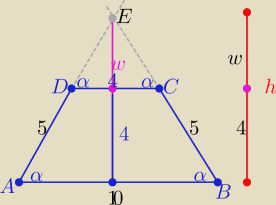
Eta: b) z podobieństwa trójkątów z cechy(kkk) w skali k>0

	10		5
k=		=
	4		2

5		h		5		w+4		8
	=		⇒		=		⇒ w=
2		w		2		w		3

	20		1
to P(ABF)=5*h= 5*		=		*100
	3		3

pole kwadratu o boku długości 10: jest równe P□ =100 zatem ................ mamy tezę

OM#62;: Dziękuję

Eta: Na zdrowie ....