335 pies: oblicz granice : Lim x→1 od strony lewej {x²+1}/{x²+3x−4} to trzeba obliczyc pochodna ilorazu ?

Janek191:

	x2 + 1		x2 + 1
f(x) =		=
	x2 + 3 x − 4		( x + 4)*(x −1)

więc lim f(x) = − ∞ x→1⁻

pies: noo ale pochodna

Janek191: Jaka pochodna ?

pies: no prosze oblicz to pochodna bo ja tak zawsze licze ....

Jack: pochodna z granicy? ;x

pies: no lol zawsze sie tak robi tak matemaks robi wiec i ja lol

Janek191:

	0
Regułę de l' Hospitala stosujemy , gdy mamy symbol nieoznaczony, np,
	0

Jack: lol........................

pies: no lol fajnie ze sie ciagle dowiaduje ze czegos nowego...ech nie mam sie gdzie nauczyc znacie jakas strone zeby sie nauczyc granice obliczlac lewo i prawostronna a co do pochodnej to przeciez zawsze jest przez 0 a jak nie to sie wstawia liczbe i tez wychodzi lol ....no ale te lewostronne i prawo .. zancie jakas strone na interencie bo nigdzie nei ma

Janek191:

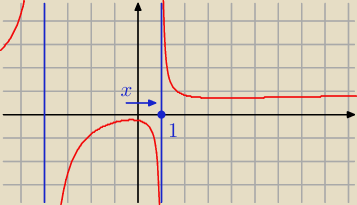
pies: ale to co mam sobie wyobrazac za kazdym razem funkcje?

Janek191: Patrz na zapis z 18.39 Jak x → 1⁻ ( czyli iksy są mniejsze od 1) to licznik → 1² + 1 = 2 Mianownik dąży do (1 + 4)*( 1 − 1) → 0 przez wartości ujemne zatem

2
	= − ∞
− 4*0

Janek191: Ten wykres miał Ci pokazać,że ta granica jest równa −∞

olekturbo: lol

pies: nie rozumiem 2/0 dlaczego do −oo a nie np.do 0 albo no nie wiem nie rozumiem tego ...nie masz jakies strony z takimi zad?

olekturbo: bo to nie jest 0 tylko 0⁻. Podstaw sobie w mianowniku w (x−1) za x liczbę troszkę mniejszą od 1 czyli np 0,9. 0,9 −1 = −0,1

2
	= −∞
0−

lol

Janek191: 2 : ( −0,0001) = ? 2 : ( − 0, 00000000 1) = ? 2 : ( − 0,000000000000000000000001) = ? itd.

pies: chwilka jak by niebylo tego − lewej strony to odp byloby 0?

pies: ja tylko umiem obliczac ja nie ma podane lewo czy prawostronnie....macie jakas strone ?

olekturbo: Nie. To wtedy musisz rozlozyc na granice lewo− i prawo− stronną

olekturbo: jak masz ⁻ to lewostronna jak ⁺ to prawo

pies: :(

pies: a jakby wmianowniku wyszlo cos innego niz 0 ..ilewostronna to ta granice mozna policzyc podstawiajac pod x?

pies: ej ma ktos cos jakas strone z takimi zad / teoria

Janek191: W mianowniku nie może wyjść coś innego niż 0, bo x → x_o i x_o ∉ Df W tym zadaniu x₀ = 1 ∉ Df lim x − x₀ = 0 x→x₀ Oblicz lim f(x) x→ −4⁻

pies: jak nie moze byc lim x−>2 z ^x3−4_2x−7 to niewyczhodzi 0 w miacnowkinku

pies: nie umiem z jakiej funkcji ? f(x)

Janek191: f − funkcja z 18.34

Janek191: To policz

	x3 − 4
lim
	2 x − 7

x→3,5⁻

PrzyszlyMakler: 19:12. Janek, a skoro dąży x przez wartości ujemne, to równie dobrze mogę sobie podstawić −100 i będę miał w liczniku liczbę dodatnią i w mianowniku dodatnią, więc będzie granica dodatnia.. Też nie rozumiem tego tematu. Jest strasznie po macoszemu potraktowany.

Janek191: x → 1⁻ więc za x podstawiamy liczby < 1 , ale coraz bliższe 1 . np. 0,9 0,99 0,999 0,9999 itd Ta różnica będzie ujemna, ale coraz bliższa 0 .

PrzyszlyMakler: Rozumiem. Dzięki.

PrzyszlyMakler: Sprobuje to 20:46

PrzyszlyMakler: Licznik zawsze będzie dodatni, a w mianowniku 3,49 − 3,5 = − czyli granica −∞

Janek191: Tak

PrzyszlyMakler: Super. Dzięki. Ale jak dadzą w maju jakiś niestworzony przykład to nic nie zrobię. XD

Janek191: Takich granic raczej nie powinno być

pies: janku janku lol ale ja nie umiem tego wlasnie

pies: obliczycc kom.20.46

Janek191: PrzyszłyMakler obliczył

pies: :( nie wiem o co chodzi

Janek191: Granicę z 20.46

bartek: lol ale ja nie umiem

Janek191: To szkoda