Geometria na płaszczyźnie
max keliwin:
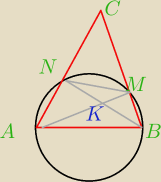
mam kłopot z tym zadaniem. Dany jest trojkat ABC. Okrąg, którego srednica jest podstawa
AB,przecina bok BC w pinkcie M, zaś bok AC w punkcie N(rysunek). Przekątne czworokąta ABMN
przecinaja się w punkcie K. Wykaż, ze prosta CK jest prostopadła do odcinka AB.
29 mar 16:47
Max Kelwin: 
29 mar 18:10
Max Kelwin: help me
29 mar 19:32
jc: BN i AM są wysokościami trójkąta ABC. Wysokości trójkąta przecinają się w jednym
punkcie K. Dlatego CK jest trzecią wysokością.
29 mar 19:43
Max Kelwin: a jak to wykazać ?
29 mar 19:45
Max Kelwin: wiem, ze tam w tych dwoch miejscach bedzie kąt prosty bo są oparte na srednicy ale dalej to nie
wiem/
29 mar 19:46
Janek191:
Dlatego to są wysokości Δ ABC
29 mar 19:52
Max Kelwin: no tak ale dlaczego ta prosta CK jest prostopadła do AB? bo nie wiem jak to wykazać, ze prosta
przechodząca przez punkt K bedzie tez wysokoscia czyli ze bedzie pod kątem prostym
29 mar 19:56
Janek191:
Dlatego, że jest trzecią wysokością .
Przechodzi przez punkt K, a w tym punkcie przecinają się wszystkie wysokości Δ.
29 mar 19:59
Max Kelwin: no oki dzięki
czyli takie uzasadnienie wystarczy ?
29 mar 20:04