2 zadania, z granicą i z funkcją Zajżeg: 1. Granica lim x−>(1/4) (4x − 1)/(2√x − 1) jest równa: A. 0.5 B. 1 C. 2 D. 4 2. Wyznacz największą liczbę naturalną n, dla której pochodna funkcji f(x) = 4x³ − 39x² spełnia warunek f'(x) < 0. pochodna wyszła mi 12x²−78x, a miejsca zerowe −6.5, 0. Nie wiem co zrobić Bardzo proszę o w miarę najprostsze wytłumaczenie obu zadań

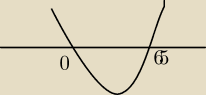
Jerzy: jaka jest najwieksza liczba naturalna w tym przedziale ?

Zajżeg: 6

Zajżeg: ale jak do tego dojść? jak robiłem to przedział miałem (−6.5 ; 0)

pytajnik123: 12x²−78x=x(12x−78)=0 ⇒ x=0 x=6,5 f'(x)>0 x∊(−∞,0) u (6,5 ; +∞) f'(x)<0 x∊(0, 6,5) ⇒ z tego wynika że "n" spełniający warunek równy jest 6

Zajżeg: Dzięki, nie przyszło mi do głowy, żeby x wyciągnąć przed nawias. A w pierwszym ktoś mógłby pomóc?

Janek191:

	( 2 √x − 1)*(2√x + 1)
f(x) =		= 2 √x + 1
	2√x − 1

więc lim f(x) = 2*√0,25 + 1 = 2*0,5 + 1 = 2 x→ ¹₄

Zajżeg: Dziękuje. Ratujecie życie