ostrosłup Ola: Podstawą ostrosłupa jest trójkąt o bokach długości 6,5 i 5.Ściany boczne tego ostrosłupa są nachylone do płaszczyzny podstawy pod kątem 45∘.Oblicz objętość tego ostrosłupa.

kochanus_niepospolitus: no i w czym problem

kochanus_niepospolitus: 1) skoro boki podstawy to 6, 5 i 5 ... to jest to trójkąt równoboczny ... policzenie jego pola nie jest trudne (zwłaszcza że wysokość opuszczona na najdłuższy bok to będzie 4) 2) skoro ściany boczne są pod kątem 45^o to korzystając z funkcji trygonometrycznych jesteś w stanie wyliczyć wysokość ściany bocznej (najszybciej −−− tej przy najdłuższym boku podstawy) − pomocna będzie długość wysokości podstawy 3) mając wysokość ściany bocznej ... wykorzystując ten sam kąt 45^o jesteś w stanie wyznaczyć wysokość ostrosłupa 4) podstawiasz do wzoru na objętość

Jerzy: równoboczny to on nie jest

kochanus_niepospolitus: ciiii ... równoramienny miało być ... myślałem że nikt nie zauważy

Ola: nie rozumiem jak obliczyc wysokość ściany bocznej

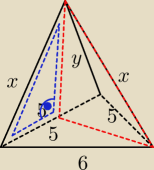
kochanus_niepospolitus: w sumie to się trochę pośpieszyłem ... łatwiej będzie wyliczyć wysokość ściany bocznej przy jednym z krótszych boków z czerwonego masz pierwsze równanie (tw. cosinusów):

	5√3		5√3
x2 = (		)2 + h2sciany bocznej − 2		*hs.b.cos45o
	2		2

z niebieskiego masz drugie równianie (tw. Pitagorasa):

	5
x2 = (		)2 + h2sciany bocznej
	2

stąd wychodzi:

	5		5√3		5√3
(		)2 + h2s.b. = (		)2 + h2s.b. − 2		*hs.b.cos45o
	2		2		2

	5		5√3		5√3
(		)2 = (		)2 − 2		*hs.b.cos45o
	2		2		2

	4		√2
1 = 3 −		hs.b.
	5		2

	5
hs.b. = 2 *		* √2 = ....
	4

na spokojnie sprawdź przekształcenia

dero2005: Podstawa jest trójkątem równoramiennym o bokach podstawa a = 6 ramiona b = 5 h − wysokość na najkrótszy bok z Pitagorasa wynosi 4

	a*h
pole podstawy wynosi		= 12
	2

	a*h		3
Obliczasz promień okręgu wpisanego w podstawę ze wzoru r =		=
	a+2b		2

Obliczysz wysokość ostrosłupa H ze wzoru (spodek wysokości wypada w środku okręgu wpisanego w podstawę)

	H
H =		= tg45o = 1
	r

	3
H = r =
	2

Obliczasz objętość

Ola: wynik nie zgadza się z odpowiedziami

kochanus_niepospolitus: dero .... wysokośc na najdłuższy bok będzie równa 4 (bo wtedy przeciwprostokątna będzie równa 5)

kochanus_niepospolitus: druga sprawa −−− czym jest r

kochanus_niepospolitus:

	12
ja oczywiście źle wyliczyłem wysokość podstawy na krótszy bok wynosi ona (oczywiście)
	5

dero2005: a = 6 b = 5 h = √b² − (^a₂)² = 4

	a*h
Pp =		= 12
	2

	r
Pp =		(a+2b) = 12
	2

	3
r =
	2

H
	= tg45o = 1
r

	3
H = r =
	2

	Pp*H
V =		= 6
	3