logarytmy kapral: Udowodnij ze jeśli log(1/3) a*log(1/3) b=4 to a*b jest mniejsze badż równe 1/81. (1/3 jest podstawą logarytmu)

kapral: Prosze o pomoc , bardzo pilne

Janek191: log_¹3 a * log_¹3 b = 4 −log₃ a * ( − log₃ b) = 4 log₃ a* log₃ b = 4

	4
x*y = 4 ⇒ y =
	x

3^x = a 3^y = b a*b = 3^x*3^y = 3^{x + y} = 3^{x + 4_x}

Ola: Mógłby mi ktoś wyjaśnić w jaki sposób to udowadnia teze?

Ola: ? Prosze o pomoc

Ola: Heeelp

Janek191:

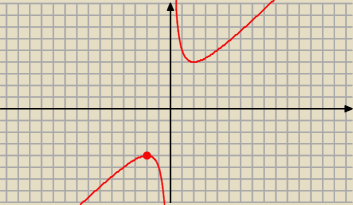
	4
Niech f(x) = x +		; x ≠ 0
	x

	4
f '(x) = 1 −		= 0 ⇔ x = − 2 lub x = 2
	x2

	8
f ''(x) = ( − 4 x−2 )' = 8 x−3 =
	x3

więc f ''(−2) = − 1 < 0 funkcja f osiąga maksimum lokalne równe y_min = − 4

	4
czyli x +		≤ − 4
	x

	1
3 x + 4x ≤ 3−4 =
	81

x = − log₃ a < 0 i y = − log₃ b < 0

Ola: Dziekuje bardzo 😀

Janek191: Tam powinno być y_max = − 4