Trójkąt prostokatny
Lola: W trójkącie prostokątnym ABC długości ramion AB i BC są równe. Z wierzchołka kąta prostego
poprowadzono dwie proste dzielące ten kąt na trzy równe części i wyznaczające na
przeciwprostokątnej punktu E i F. Oblicz długość odcinków AE,EF,FC jeżeli długość
przeciwprostokątnej jest równa 8√2
29 mar 09:40
kochanus_niepospolitus:
Weź się za te zadania co zrobiłaś a nie wpisujesz co rusz kolejne
29 mar 09:40
Lola: spokojnie, ogarnięte..
29 mar 17:07
Matej:
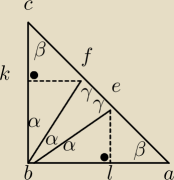
Odświeżam, dziś dostałem to samo zadanie. Rozrysowałem i widzę zależności. Wiemy,że α=30, β=45
a γ=75.Nie mam pojęcia jak to rozwiązać. Obliczyć pole całego trójkąta i z podobieństwa
wyznaczyć odcinki |KF|=|LE| ? Proszę o pomoc.
PS. Sorry za słaby rysunek.
1 kwi 17:35
Rafal44: EF=x
BF=BE=y
AE=CF=z
Z twierdzenia cosinusów dla trójkąta EBF:
| | √3 | |
x2=y2+y2−2y2cos30=2y2−2y2* |
| =2y2−√3y2 |
| | 2 | |
Z twierdzenia cosinusów dla trójkąta BAE:
| | √3 | |
z2=82+y2−2*8*y*cos30=64+y2−16y* |
| =64+y2−8√3y |
| | 2 | |
Z twierdzenia o dwusiecznej dla trójkąta BAF:
| 2y2−√3y2 | | y2 | |
| = |
| /:y2 |
| 64+y2−8√3y | | 64 | |
128−64
√3=64+y
2−8
√3y
y
2−8
√3y+64
√3−64=0
1 kwi 18:43
Matej: Dzięki

1 kwi 19:18
Rafal44: Δ=192−256
√3+256=448−256
√3=64(7−4
√3)=64(4−4
√3+3)=64(2−
√3)
2
√Δ=8(2−
√3)=16−8
√3
| | 8√3−16+8√3 | |
y1= |
| =8√3−8=8(√3−1) |
| | 2 | |
| | 8√3+16−8√3 | |
y2= |
| =8 (sprzeczność, gdyż trójkąt BAE nie ma równych ramion BA i BE) |
| | 2 | |
x
2=y
2(2−
√3)=64(4−2
√3)(2−
√3)=128(2−
√3)
2
x=8
√2(2−
√3)=16
√2−8
√6
| | 8√2−x | | 8√2−16√2+8√6 | |
z= |
| = |
| =4√6−4√2 |
| | 2 | | 2 | |
1 kwi 19:21
Rafal44: OK., jestem idiotą. Można było kilkulinijkowo z podobieństwa.
1 kwi 19:28
Rafal44: Niech LE=a. Wtedy BL=a√3 i AL=a, czyli 8=BA=BL+AL=a√3+a=a(√3+1)⇔a=U{8(√3−1){2}.
Wobec tego BE=2a=8(√3−1)
1 kwi 19:32
Rafal44: | | 8(√3−1) | |
A co najważniejsze, AE=a√2= |
| *√2=4(√3−1)*√2=4√6−4√2 |
| | 2 | |
1 kwi 19:38
Mila:
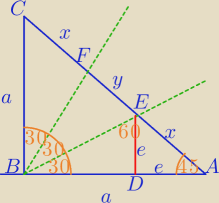
1)
|AC|=8
√2
a=8
|AE|=e
√2
|BD|=e
√3
2)
e
√3+e=8
e*(
√3+1)=8 /*(
√3−1)
e=4*(
√3−1)
|AE|=4*(
√3−1)*
√2⇔
|AE|=4(√6−√2)
|FE|=8
√2−8(
√6−
√2)=16
√2−8
√6⇔
|FE|=8(2√2−√6)
================
1 kwi 22:15
 Odświeżam, dziś dostałem to samo zadanie. Rozrysowałem i widzę zależności. Wiemy,że α=30, β=45
a γ=75.Nie mam pojęcia jak to rozwiązać. Obliczyć pole całego trójkąta i z podobieństwa
wyznaczyć odcinki |KF|=|LE| ? Proszę o pomoc.
PS. Sorry za słaby rysunek.
Odświeżam, dziś dostałem to samo zadanie. Rozrysowałem i widzę zależności. Wiemy,że α=30, β=45
a γ=75.Nie mam pojęcia jak to rozwiązać. Obliczyć pole całego trójkąta i z podobieństwa
wyznaczyć odcinki |KF|=|LE| ? Proszę o pomoc.
PS. Sorry za słaby rysunek.

 1)
|AC|=8√2
a=8
|AE|=e√2
|BD|=e√3
2)
e√3+e=8
e*(√3+1)=8 /*(√3−1)
e=4*(√3−1)
|AE|=4*(√3−1)*√2⇔
|AE|=4(√6−√2)
|FE|=8√2−8(√6−√2)=16√2−8√6⇔
|FE|=8(2√2−√6)
================
1)
|AC|=8√2
a=8
|AE|=e√2
|BD|=e√3
2)
e√3+e=8
e*(√3+1)=8 /*(√3−1)
e=4*(√3−1)
|AE|=4*(√3−1)*√2⇔
|AE|=4(√6−√2)
|FE|=8√2−8(√6−√2)=16√2−8√6⇔
|FE|=8(2√2−√6)
================