Równanie kwadratowe z parametrem
CienkiBolek: Dla jakiej wartości parametru "k" oba pierwiastki równania:
x2 + (2k+6)x + 4k + 12 = 0
są większe od −1
Wiadomo, że Δ musi być większa od 0 no to mam
k2 + 2k − 3 > 0
no i k ∊ (−oo; −3) ∪ (1; +oo)
Dalej próbowałem zawęzić przedziały szukając z równań na pierwiastki x1 i x2 oraz ze wzorów
Viete'a − i nic
28 mar 23:57
Dżin:
x
1>−1 → x
1+1>0
x
2>−1 → x
2+1>0
Iloczyn większy niż 0:
(x
1+1)(x
2+1)>0 → x
1x
2+x
1+x
2+1>0
Suma większa niż 0:
x
1+x
2+2>0
Dalej już z Viete'y

29 mar 00:07
rybka:
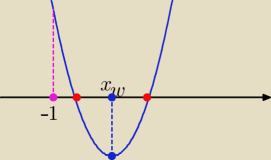
1/ Δ>0
2/ f(−1)>0
29 mar 00:08
CienkiBolek: Dżin − coś nie wychodzi z twoich danych.
rybka − twoje dane są Ok bo w rozwiązaniach mam k∊(−3,5; −3)
29 mar 00:39

 1/ Δ>0
2/ f(−1)>0
1/ Δ>0
2/ f(−1)>0