Wartość bezwzględna, parametr, 4 dodatnie rozwiązania maturzysta16: Równanie |(x−3)²−5|=m ma cztery dodatnie rozwiązania wtedy i tylko wtedy gdy: A) m∊(0;2); B) m∊(0;3); C) m∊(0;4); D) m∊(0;5);

5-latek : Narysuj wykres funkcji y=|(x−3)³−5 | i tnij go prosta y=m

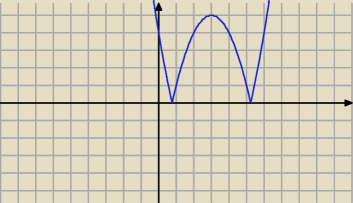
5-latek : Myslaem ze nie trzeba będzie rysować wykresu tyko spojrzeć na wierzchołek tej funkcji i będzie odp D) Jednak nie będzie tak należy wyznaczyć punkt przecięcia wykresu z osia OY i dopiero odczytac rozwiązanie

maturzysta16: Dzięki widać że m∊(0;4) a jak inaczej można się za to zabrać

maturzysta16: D?

5-latek : Pomysl

maturzysta16: Mój błąd, masz racje

5-latek : Rozwiazanie podales dobre . Pomysl to było do tego jak to się zabrać do tego inaczej

5-latek : dobre to m∊(0,4)

maturzysta16: wyszłoby jeśliby skorzystać z warunków że Δ>0 x1+x2>0 i x1−x2>0 dla (x−3)²−5=m i (x−3)²−5=−m ? czy nie tym tropem?

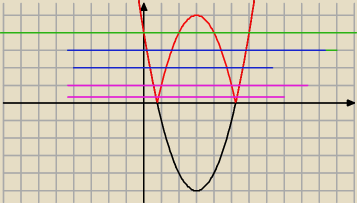
5-latek : Nie tym tropem tylko tak jak napisałem myslec. NIc na sile tylko młotkiem Żeby to równanie miało 4 rozwiązania dodatnie to te rozwiązania musze lezec na prawo od osi OY . Tak ? Zgadza się ? Wierzzcholek funkcji y=(x−3)²−5 ma wspolrzedne (3,−5) Natomiast wierzchołek funkcji y=|(x−3)²−5| ma wspolrzedne (3.5) to wiadomo dlaczego ? Wiec wydawac by się moglo ze będzie odpowiedz D . Jednak nie Te rozwiązania musz zlezec po punktem przciecia wykresu z osia oy wtedy sa dodatnie Liczymy punkt przecia się wykresu y=(x−3)²−5 z osia OY wiemy ze x=0 y=(0−3)²−5=9−5=4 Punkt przciecia się z osia OY ma wspolrzedne (0,4) Wiec wierzchołek jest wyżej niż punkt (0,4) dlatego rozwiaazaniem jest C)

5-latek : Zauwaz ze dla y=4 nie masz wszystkich rozwiazan dodatnich

maturzysta16: No tak, dlatego otwarty przedział. Dzięki za przypomnienie Pozdrawiam!

5-latek : Na zdrowie